Loop estimator for discounted values in Markov reward processes

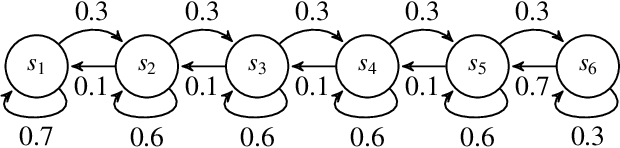
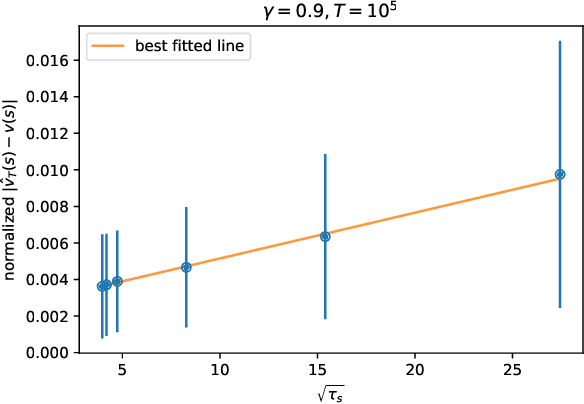
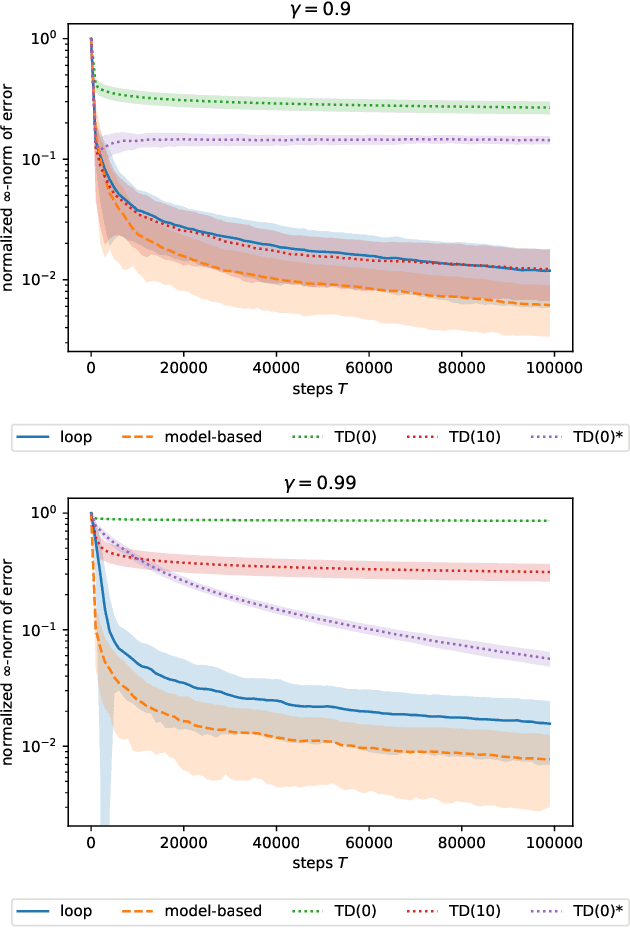
At the working heart of policy iteration algorithms commonly used and studied in the discounted setting of reinforcement learning, the policy evaluation step estimates the value of state with samples from a Markov reward process induced by following a Markov policy in a Markov decision process. We propose a simple and efficient estimator called \emph{loop estimator} that exploits the regenerative structure of Markov reward processes without explicitly estimating a full model. Our method enjoys a space complexity of $O(1)$ when estimating the value of a single positive recurrent state $s$ unlike TD (with $O(S)$) or model-based methods (with $O(S^2)$). Moreover, the regenerative structure enables us to show, without relying on the generative model approach, that the estimator has an instance-dependent convergence rate of $\widetilde{O}(\sqrt{\tau_s/T})$ over steps $T$ on a single sample path, where $\tau_s$ is the maximal expected hitting time to state $s$. In preliminary numerical experiments, the loop estimator outperforms model-free methods, such as TD(k), and is competitive with the model-based estimator.