Locally Imposing Function for Generalized Constraint Neural Networks - A Study on Equality Constraints
Paper and Code
Apr 18, 2016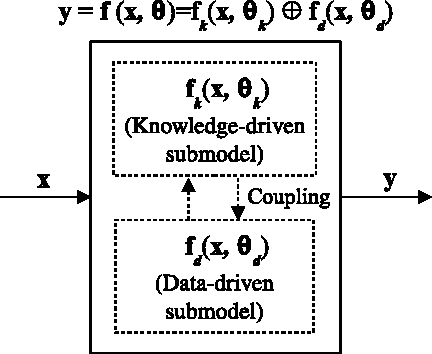
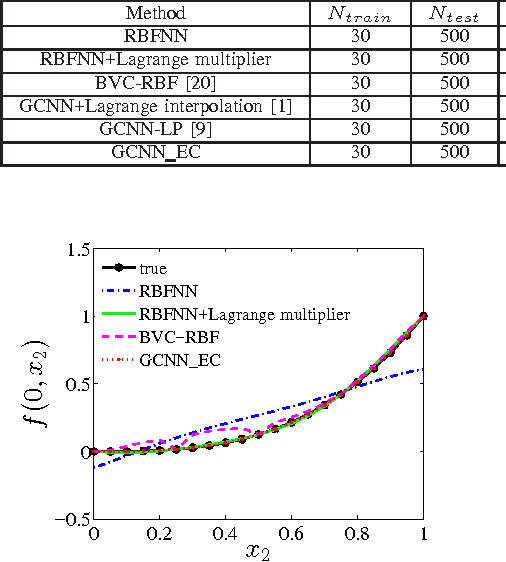

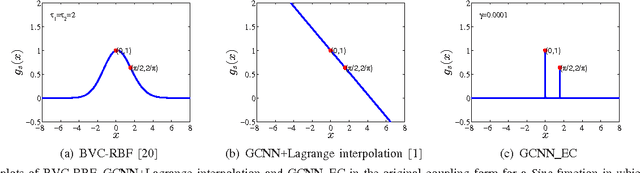
This work is a further study on the Generalized Constraint Neural Network (GCNN) model [1], [2]. Two challenges are encountered in the study, that is, to embed any type of prior information and to select its imposing schemes. The work focuses on the second challenge and studies a new constraint imposing scheme for equality constraints. A new method called locally imposing function (LIF) is proposed to provide a local correction to the GCNN prediction function, which therefore falls within Locally Imposing Scheme (LIS). In comparison, the conventional Lagrange multiplier method is considered as Globally Imposing Scheme (GIS) because its added constraint term exhibits a global impact to its objective function. Two advantages are gained from LIS over GIS. First, LIS enables constraints to fire locally and explicitly in the domain only where they need on the prediction function. Second, constraints can be implemented within a network setting directly. We attempt to interpret several constraint methods graphically from a viewpoint of the locality principle. Numerical examples confirm the advantages of the proposed method. In solving boundary value problems with Dirichlet and Neumann constraints, the GCNN model with LIF is possible to achieve an exact satisfaction of the constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge