Localized epidemic detection in networks with overwhelming noise
Paper and Code
Feb 06, 2014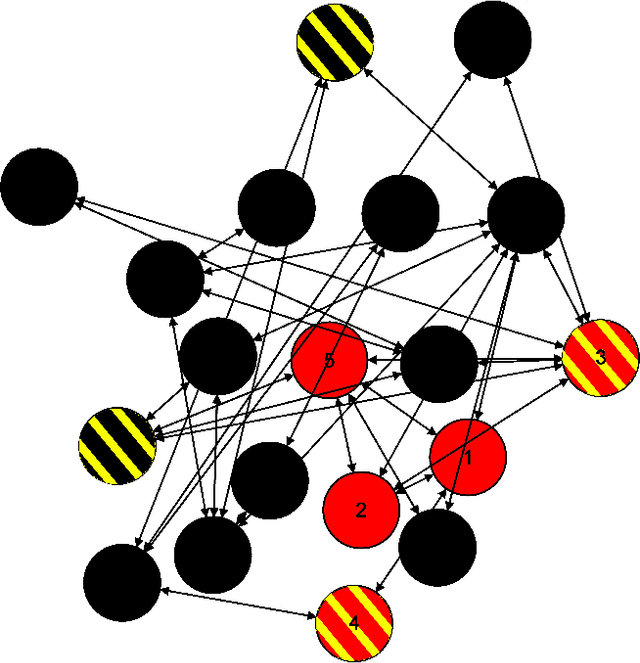


We consider the problem of detecting an epidemic in a population where individual diagnoses are extremely noisy. The motivation for this problem is the plethora of examples (influenza strains in humans, or computer viruses in smartphones, etc.) where reliable diagnoses are scarce, but noisy data plentiful. In flu/phone-viruses, exceedingly few infected people/phones are professionally diagnosed (only a small fraction go to a doctor) but less reliable secondary signatures (e.g., people staying home, or greater-than-typical upload activity) are more readily available. These secondary data are often plagued by unreliability: many people with the flu do not stay home, and many people that stay home do not have the flu. This paper identifies the precise regime where knowledge of the contact network enables finding the needle in the haystack: we provide a distributed, efficient and robust algorithm that can correctly identify the existence of a spreading epidemic from highly unreliable local data. Our algorithm requires only local-neighbor knowledge of this graph, and in a broad array of settings that we describe, succeeds even when false negatives and false positives make up an overwhelming fraction of the data available. Our results show it succeeds in the presence of partial information about the contact network, and also when there is not a single "patient zero", but rather many (hundreds, in our examples) of initial patient-zeroes, spread across the graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge