Localization Algorithm with Circular Representation in 2D and its Similarity to Mammalian Brains
Paper and Code
Jan 25, 2019
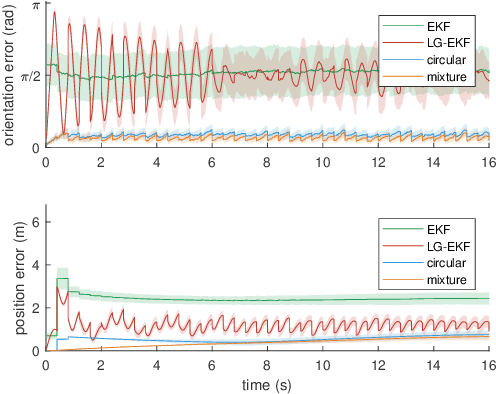
Extended Kalman filter (EKF) does not guarantee consistent mean and covariance under linearization, even though it is the main framework for robotic localization. While Lie group improves the modeling of the state space in localization, the EKF on Lie group still relies on the arbitrary Gaussian assumption in face of nonlinear models. We instead use von Mises filter for orientation estimation together with the conventional Kalman filter for position estimation, and thus we are able to characterize the first two moments of the state estimates. Since the proposed algorithm holds a solid probabilistic basis, it is fundamentally relieved from the inconsistency problem. Furthermore, we extend the localization algorithm to fully circular representation even for position, which is similar to grid patterns found in mammalian brains and in recurrent neural networks. The applicability of the proposed algorithms is substantiated not only by strong mathematical foundation but also by the comparison against other common localization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge