Local Permutation Equivariance For Graph Neural Networks
Paper and Code
Nov 23, 2021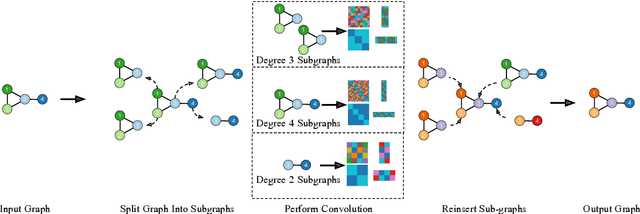
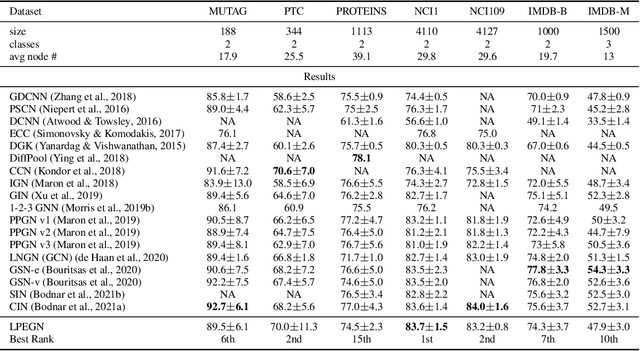

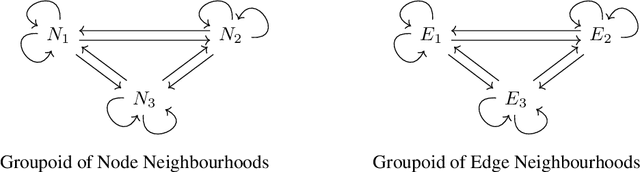
In this work we develop a new method, named locally permutation-equivariant graph neural networks, which provides a framework for building graph neural networks that operate on local node neighbourhoods, through sub-graphs, while using permutation equivariant update functions. Message passing neural networks have been shown to be limited in their expressive power and recent approaches to over come this either lack scalability or require structural information to be encoded into the feature space. The general framework presented here overcomes the scalability issues associated with global permutation equivariance by operating on sub-graphs through restricted representations. In addition, we prove that there is no loss of expressivity by using restricted representations. Furthermore, the proposed framework only requires a choice of $k$-hops for creating sub-graphs and a choice of representation space to be used for each layer, which makes the method easily applicable across a range of graph based domains. We experimentally validate the method on a range of graph benchmark classification tasks, demonstrating either state-of-the-art results or very competitive results on all benchmarks. Further, we demonstrate that the use of local update functions offers a significant improvement in GPU memory over global methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge