Local Nonparametric Meta-Learning
Paper and Code
Feb 09, 2020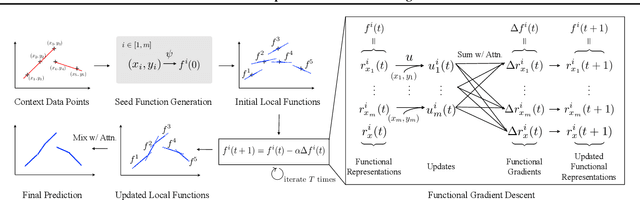
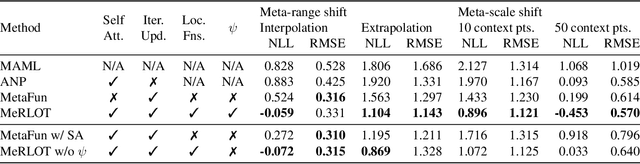
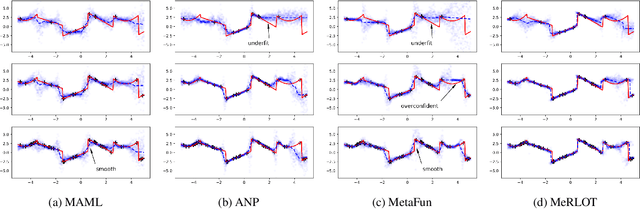
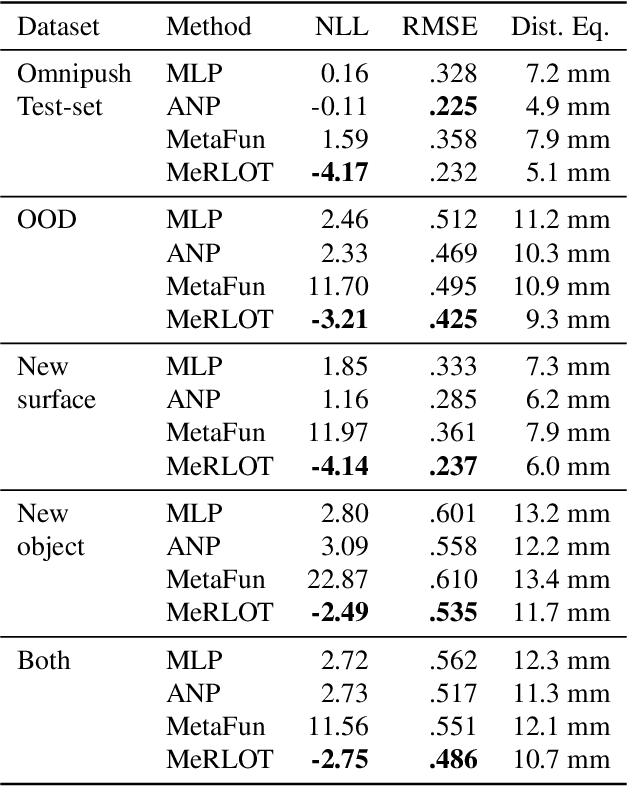
A central goal of meta-learning is to find a learning rule that enables fast adaptation across a set of tasks, by learning the appropriate inductive bias for that set. Most meta-learning algorithms try to find a \textit{global} learning rule that encodes this inductive bias. However, a global learning rule represented by a fixed-size representation is prone to meta-underfitting or -overfitting since the right representational power for a task set is difficult to choose a priori. Even when chosen correctly, we show that global, fixed-size representations often fail when confronted with certain types of out-of-distribution tasks, even when the same inductive bias is appropriate. To address these problems, we propose a novel nonparametric meta-learning algorithm that utilizes a meta-trained local learning rule, building on recent ideas in attention-based and functional gradient-based meta-learning. In several meta-regression problems, we show improved meta-generalization results using our local, nonparametric approach and achieve state-of-the-art results in the robotics benchmark, Omnipush.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge