Local Distribution Obfuscation via Probability Coupling

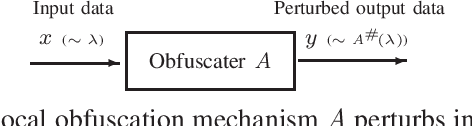
We introduce a general model for the local obfuscation of probability distributions and investigate its theoretical properties. Specifically, we relax a notion of distribution privacy by generalizing it to divergence, and investigate local obfuscation mechanisms that provide the divergence distribution privacy. To provide f-divergence distribution privacy, we prove that the perturbation noise should be added proportionally to the Earth mover's distance between the probability distributions that we want to make indistinguishable. Furthermore, we introduce a local obfuscation mechanism, which we call a coupling mechanism, that provides divergence distribution privacy while optimizing the utility of obfuscated data by using exact/approximate auxiliary information on the input distributions we want to protect.