Local Competition and Stochasticity for Adversarial Robustness in Deep Learning

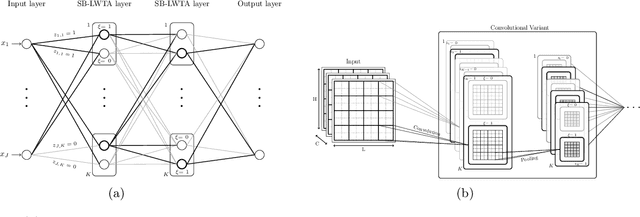
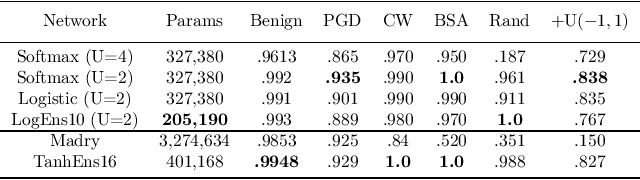
This work addresses adversarial robustness in deep learning by considering deep networks with stochastic local winner-takes-all (LWTA) nonlinearities. This type of network units result in sparse representations from each model layer, as the units are organized in blocks where only one unit generates non-zero output. The main operating principle of the introduced units lies on stochastic arguments, as the network performs posterior sampling over competing units to select the winner. We combine these LWTA arguments with tools from the field of Bayesian non-parametrics, specifically the stick-breaking construction of the Indian Buffet Process, to allow for inferring the sub-part of each layer that is essential for modeling the data at hand. Inference for the proposed network is performed by means of stochastic variational Bayes. We perform a thorough experimental evaluation of our model using benchmark datasets, assuming gradient-based adversarial attacks. As we show, our method achieves high robustness to adversarial perturbations, with state-of-the-art performance in powerful white-box attacks.