LLMs hallucinate graphs too: a structural perspective
Paper and Code
Aug 30, 2024
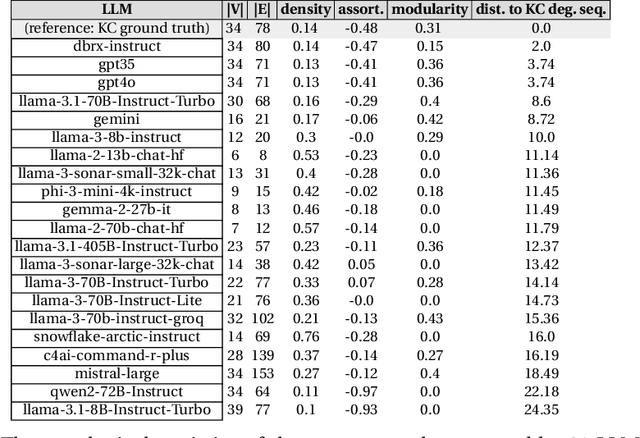

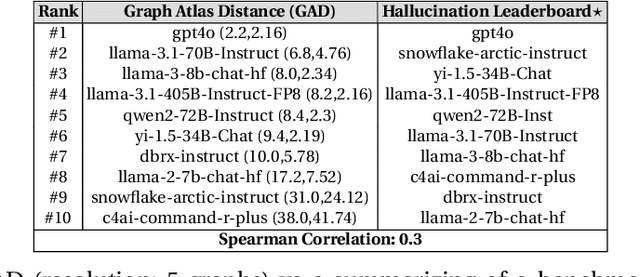
It is known that LLMs do hallucinate, that is, they return incorrect information as facts. In this paper, we introduce the possibility to study these hallucinations under a structured form: graphs. Hallucinations in this context are incorrect outputs when prompted for well known graphs from the literature (e.g. Karate club, Les Mis\'erables, graph atlas). These hallucinated graphs have the advantage of being much richer than the factual accuracy -- or not -- of a fact; this paper thus argues that such rich hallucinations can be used to characterize the outputs of LLMs. Our first contribution observes the diversity of topological hallucinations from major modern LLMs. Our second contribution is the proposal of a metric for the amplitude of such hallucinations: the Graph Atlas Distance, that is the average graph edit distance from several graphs in the graph atlas set. We compare this metric to the Hallucination Leaderboard, a hallucination rank that leverages 10,000 times more prompts to obtain its ranking.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge