LiSHT: Non-Parametric Linearly Scaled Hyperbolic Tangent Activation Function for Neural Networks

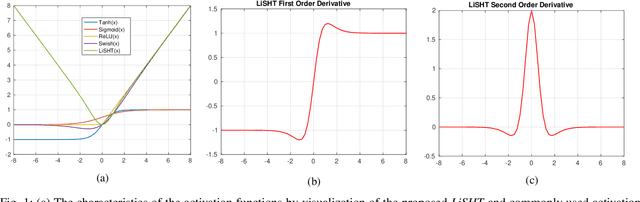
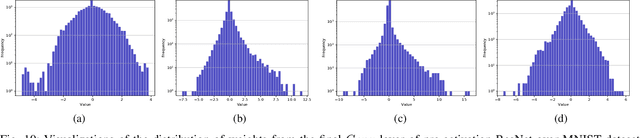
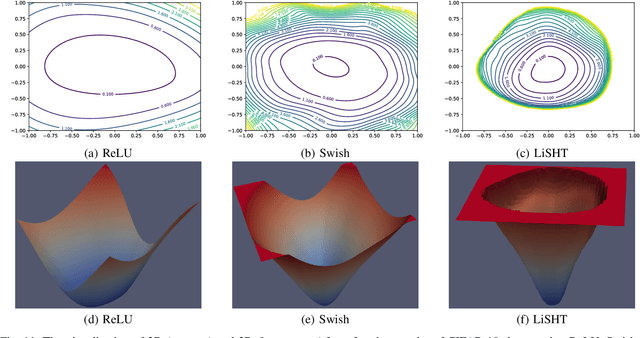
The activation function in neural network is one of the important aspects which facilitates the deep training by introducing the non-linearity into the learning process. However, because of zero-hard rectification, some the of existing activations function such as ReLU and Swish miss to utilize the negative input values and may suffer from the dying gradient problem. Thus, it is important to look for a better activation function which is free from such problems. As a remedy, this paper proposes a new non-parametric function, called Linearly Scaled Hyperbolic Tangent (LiSHT) for Neural Networks (NNs). The proposed LiSHT activation function is an attempt to scale the non-linear Hyperbolic Tangent (Tanh) function by a linear function and tackle the dying gradient problem. The training and classification experiments are performed over benchmark Car Evaluation, Iris, MNIST, CIFAR10, CIFAR100 and twitter140 datasets to show that the proposed activation achieves faster convergence and higher performance. A very promising performance improvement is observed on three different type of neural networks including Multi-layer Perceptron (MLP), Convolutional Neural Network (CNN) and Recurrent neural network like Long-short term memory (LSTM). The advantages of proposed activation function are also visualized in terms of the feature activation maps, weight distribution and loss landscape.