Lipschitz constant estimation for general neural network architectures using control tools
Paper and Code
May 02, 2024
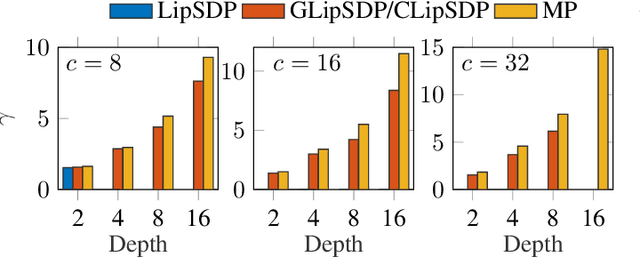
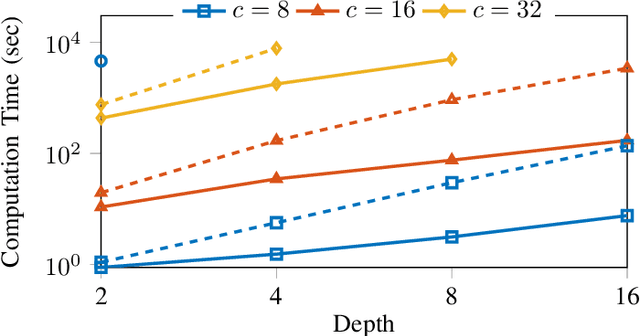
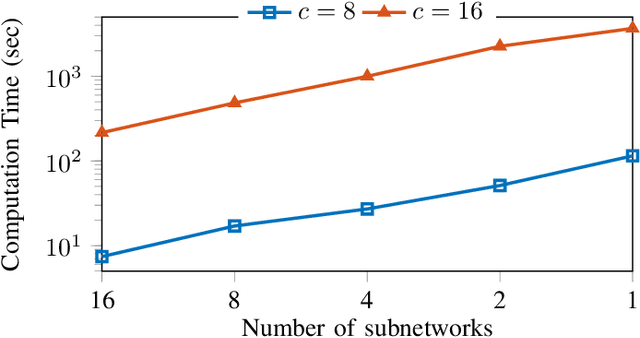
This paper is devoted to the estimation of the Lipschitz constant of neural networks using semidefinite programming. For this purpose, we interpret neural networks as time-varying dynamical systems, where the $k$-th layer corresponds to the dynamics at time $k$. A key novelty with respect to prior work is that we use this interpretation to exploit the series interconnection structure of neural networks with a dynamic programming recursion. Nonlinearities, such as activation functions and nonlinear pooling layers, are handled with integral quadratic constraints. If the neural network contains signal processing layers (convolutional or state space model layers), we realize them as 1-D/2-D/N-D systems and exploit this structure as well. We distinguish ourselves from related work on Lipschitz constant estimation by more extensive structure exploitation (scalability) and a generalization to a large class of common neural network architectures. To show the versatility and computational advantages of our method, we apply it to different neural network architectures trained on MNIST and CIFAR-10.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge