Lightweight Data Fusion with Conjugate Mappings
Paper and Code
Nov 20, 2020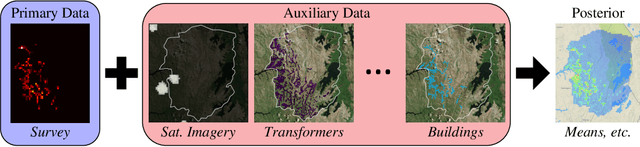
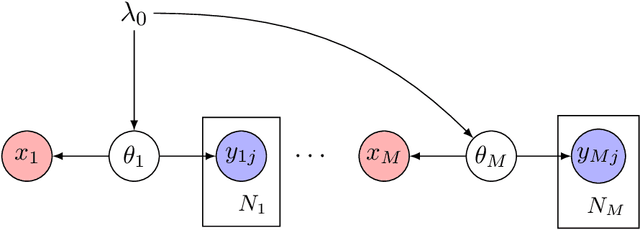

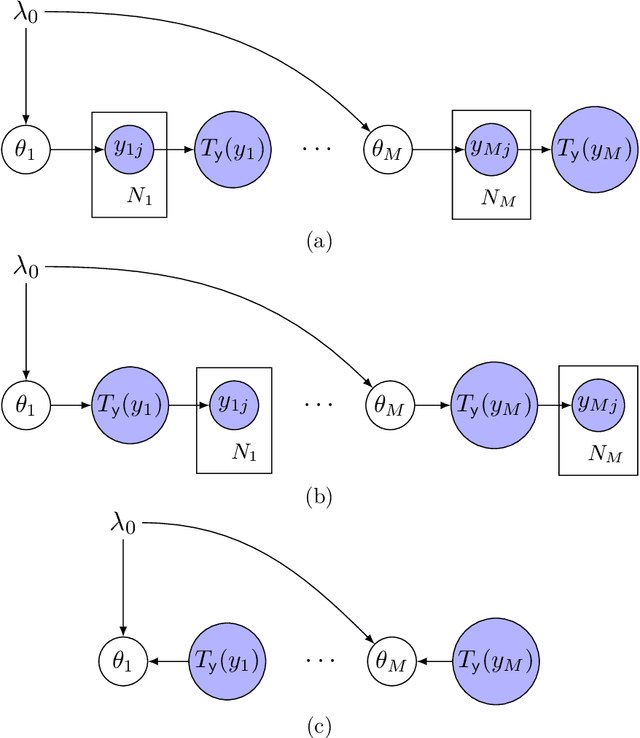
We present an approach to data fusion that combines the interpretability of structured probabilistic graphical models with the flexibility of neural networks. The proposed method, lightweight data fusion (LDF), emphasizes posterior analysis over latent variables using two types of information: primary data, which are well-characterized but with limited availability, and auxiliary data, readily available but lacking a well-characterized statistical relationship to the latent quantity of interest. The lack of a forward model for the auxiliary data precludes the use of standard data fusion approaches, while the inability to acquire latent variable observations severely limits direct application of most supervised learning methods. LDF addresses these issues by utilizing neural networks as conjugate mappings of the auxiliary data: nonlinear transformations into sufficient statistics with respect to the latent variables. This facilitates efficient inference by preserving the conjugacy properties of the primary data and leads to compact representations of the latent variable posterior distributions. We demonstrate the LDF methodology on two challenging inference problems: (1) learning electrification rates in Rwanda from satellite imagery, high-level grid infrastructure, and other sources; and (2) inferring county-level homicide rates in the USA by integrating socio-economic data using a mixture model of multiple conjugate mappings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge