Leveraging The Topological Consistencies of Learning in Deep Neural Networks
Paper and Code
Nov 30, 2021

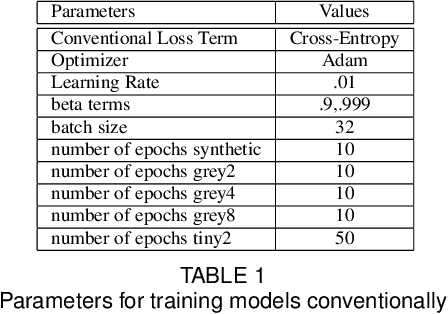
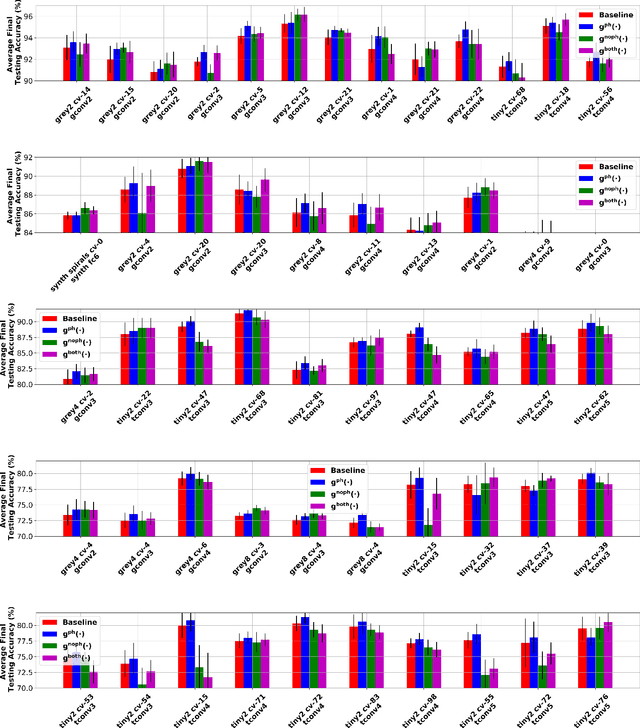
Recently, methods have been developed to accurately predict the testing performance of a Deep Neural Network (DNN) on a particular task, given statistics of its underlying topological structure. However, further leveraging this newly found insight for practical applications is intractable due to the high computational cost in terms of time and memory. In this work, we define a new class of topological features that accurately characterize the progress of learning while being quick to compute during running time. Additionally, our proposed topological features are readily equipped for backpropagation, meaning that they can be incorporated in end-to-end training. Our newly developed practical topological characterization of DNNs allows for an additional set of applications. We first show we can predict the performance of a DNN without a testing set and without the need for high-performance computing. We also demonstrate our topological characterization of DNNs is effective in estimating task similarity. Lastly, we show we can induce learning in DNNs by actively constraining the DNN's topological structure. This opens up new avenues in constricting the underlying structure of DNNs in a meta-learning framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge