Learning Two-layer Neural Networks with Symmetric Inputs
Paper and Code
Oct 16, 2018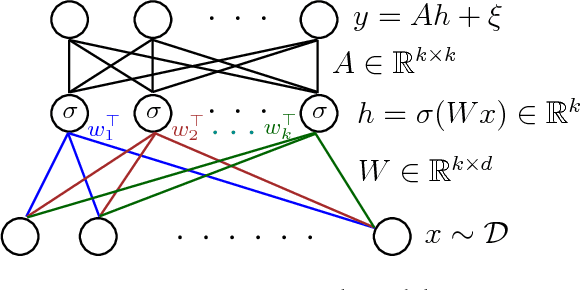

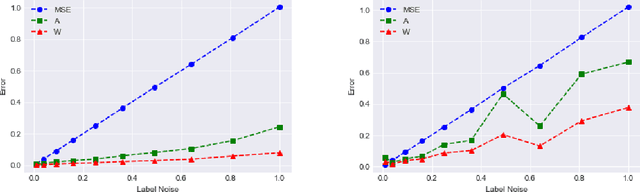
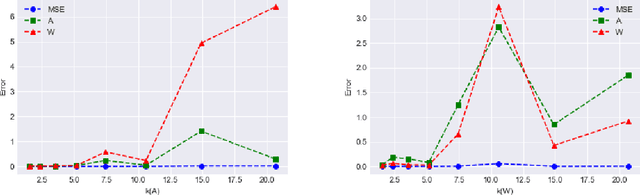
We give a new algorithm for learning a two-layer neural network under a general class of input distributions. Assuming there is a ground-truth two-layer network $$ y = A \sigma(Wx) + \xi, $$ where $A,W$ are weight matrices, $\xi$ represents noise, and the number of neurons in the hidden layer is no larger than the input or output, our algorithm is guaranteed to recover the parameters $A,W$ of the ground-truth network. The only requirement on the input $x$ is that it is symmetric, which still allows highly complicated and structured input. Our algorithm is based on the method-of-moments framework and extends several results in tensor decompositions. We use spectral algorithms to avoid the complicated non-convex optimization in learning neural networks. Experiments show that our algorithm can robustly learn the ground-truth neural network with a small number of samples for many symmetric input distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge