Learning to Schedule in Non-Stationary Wireless Networks With Unknown Statistics
Paper and Code
Aug 04, 2023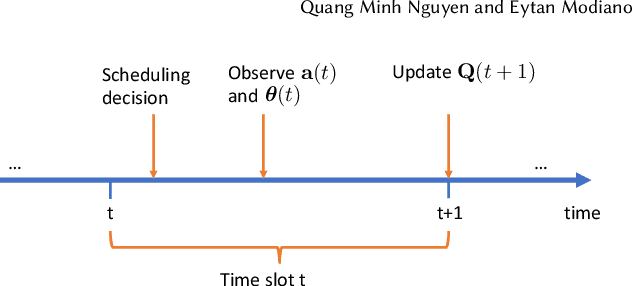
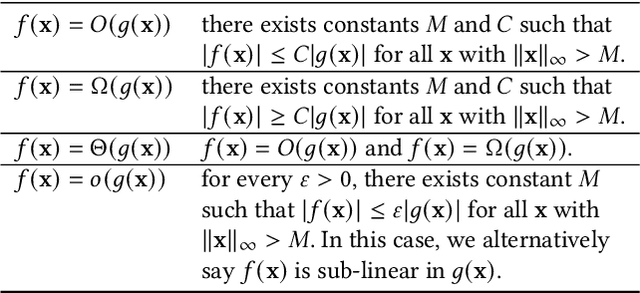
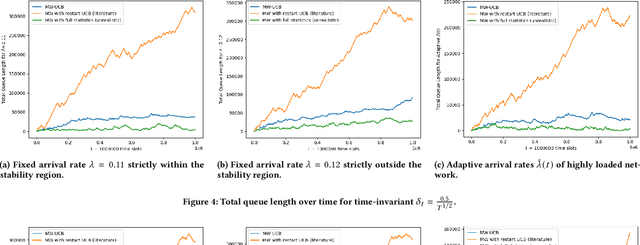
The emergence of large-scale wireless networks with partially-observable and time-varying dynamics has imposed new challenges on the design of optimal control policies. This paper studies efficient scheduling algorithms for wireless networks subject to generalized interference constraint, where mean arrival and mean service rates are unknown and non-stationary. This model exemplifies realistic edge devices' characteristics of wireless communication in modern networks. We propose a novel algorithm termed MW-UCB for generalized wireless network scheduling, which is based on the Max-Weight policy and leverages the Sliding-Window Upper-Confidence Bound to learn the channels' statistics under non-stationarity. MW-UCB is provably throughput-optimal under mild assumptions on the variability of mean service rates. Specifically, as long as the total variation in mean service rates over any time period grows sub-linearly in time, we show that MW-UCB can achieve the stability region arbitrarily close to the stability region of the class of policies with full knowledge of the channel statistics. Extensive simulations validate our theoretical results and demonstrate the favorable performance of MW-UCB.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge