Learning to Optimize Quasi-Newton Methods
Paper and Code
Oct 11, 2022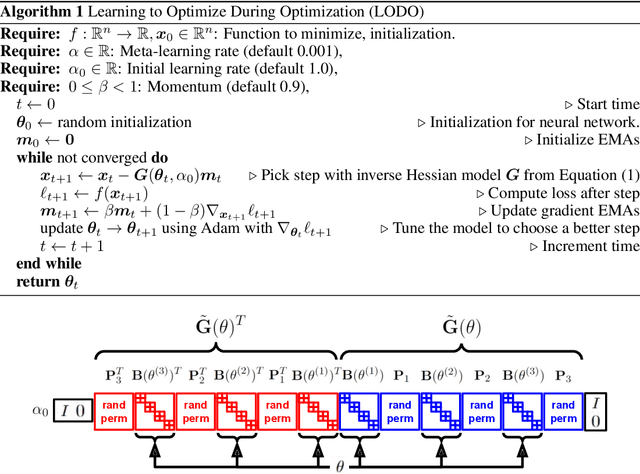
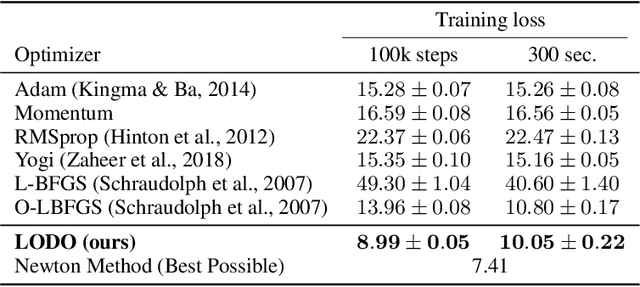
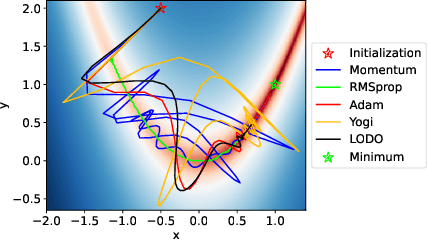
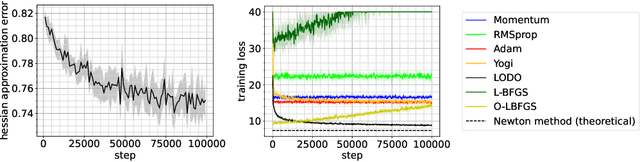
We introduce a novel machine learning optimizer called LODO, which online meta-learns an implicit inverse Hessian of the loss as a subroutine of quasi-Newton optimization. Our optimizer merges Learning to Optimize (L2O) techniques with quasi-Newton methods to learn neural representations of symmetric matrix vector products, which are more flexible than those in other quasi-Newton methods. Unlike other L2O methods, ours does not require any meta-training on a training task distribution, and instead learns to optimize on the fly while optimizing on the test task, adapting to the local characteristics of the loss landscape while traversing it. Theoretically, we show that our optimizer approximates the inverse Hessian in noisy loss landscapes and is capable of representing a wide range of inverse Hessians. We experimentally verify our algorithm's performance in the presence of noise, and show that simpler alternatives for representing the inverse Hessians worsen performance. Lastly, we use our optimizer to train a semi-realistic deep neural network with 95k parameters, and obtain competitive results against standard neural network optimizers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge