Learning to Maximize Gains From Trade in Small Markets
Paper and Code
Jan 21, 2024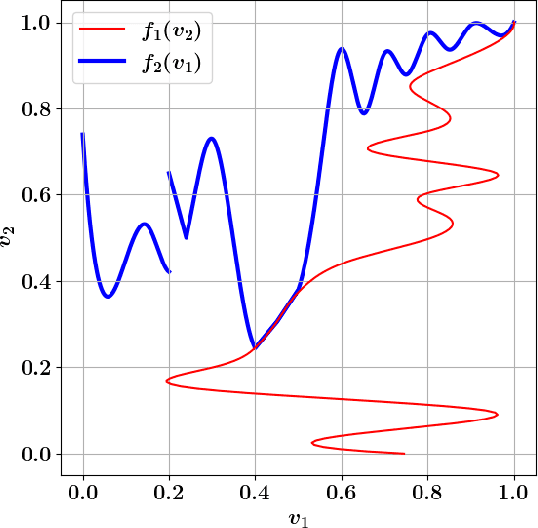
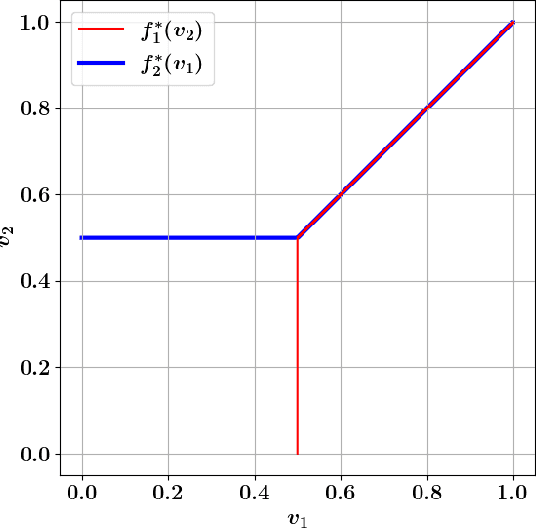
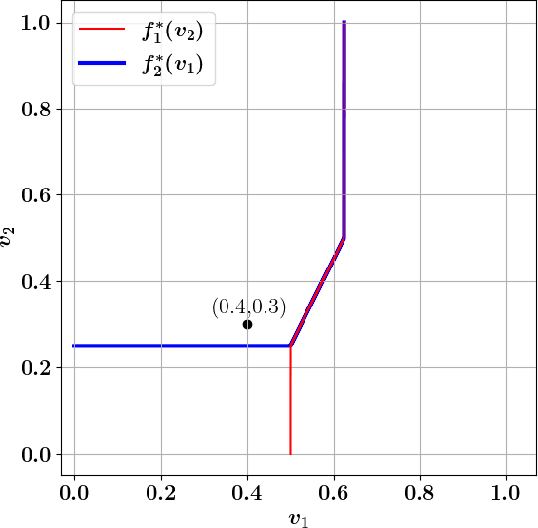
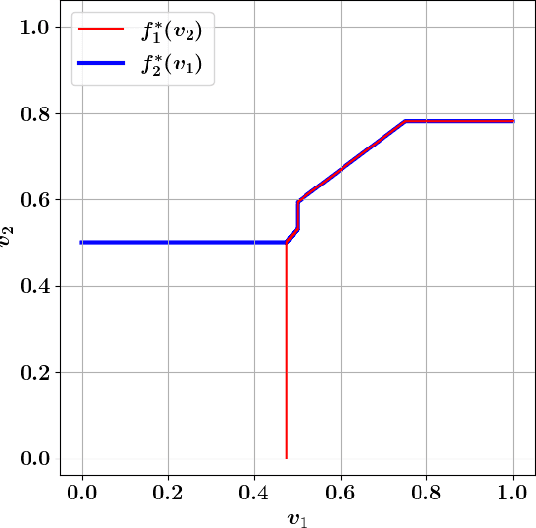
We study the problem of designing a two-sided market (double auction) to maximize the gains from trade (social welfare) under the constraints of (dominant-strategy) incentive compatibility and budget-balance. Our goal is to do so for an unknown distribution from which we are given a polynomial number of samples. Our first result is a general impossibility for the case of correlated distributions of values even between just one seller and two buyers, in contrast to the case of one seller and one buyer (bilateral trade) where this is possible. Our second result is an efficient learning algorithm for one seller and two buyers in the case of independent distributions which is based on a novel algorithm for computing optimal mechanisms for finitely supported and explicitly given independent distributions. Both results rely heavily on characterizations of (dominant-strategy) incentive compatible mechanisms that are strongly budget-balanced.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge