Learning the String Partial Order

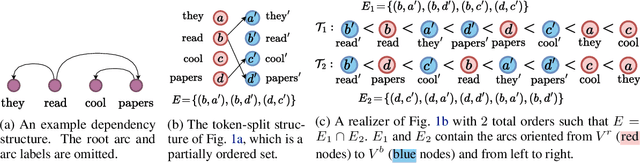
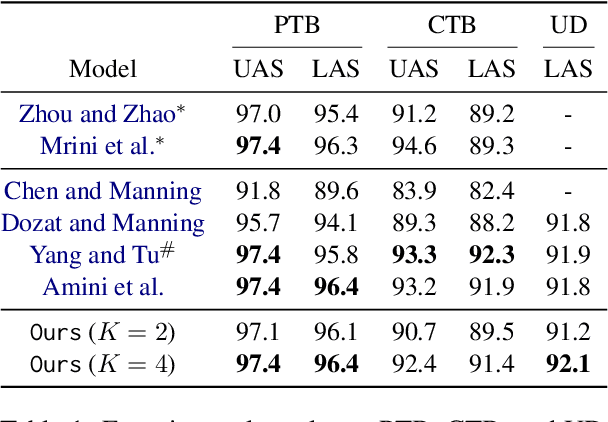
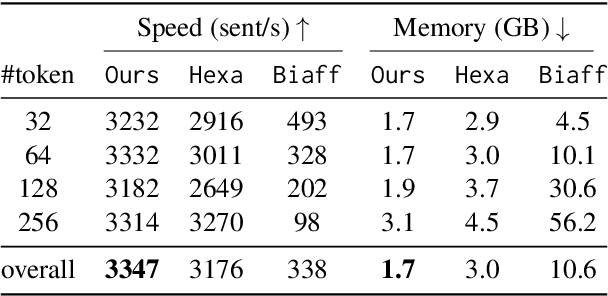
We show that most structured prediction problems can be solved in linear time and space by considering them as partial orderings of the tokens in the input string. Our method computes real numbers for each token in an input string and sorts the tokens accordingly, resulting in as few as 2 total orders of the tokens in the string. Each total order possesses a set of edges oriented from smaller to greater tokens. The intersection of total orders results in a partial order over the set of input tokens, which is then decoded into a directed graph representing the desired structure. Experiments show that our method achieves 95.4 LAS and 96.9 UAS by using an intersection of 2 total orders, 95.7 LAS and 97.1 UAS with 4 on the English Penn Treebank dependency parsing benchmark. Our method is also the first linear-complexity coreference resolution model and achieves 79.2 F1 on the English OntoNotes benchmark, which is comparable with state of the art.