Learning the Preferences of Uncertain Humans with Inverse Decision Theory

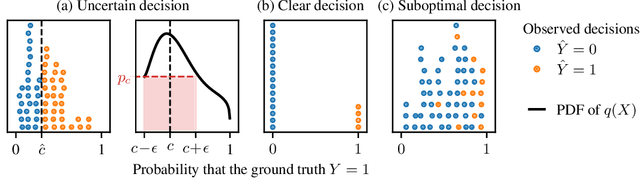
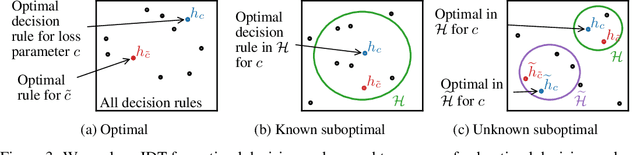
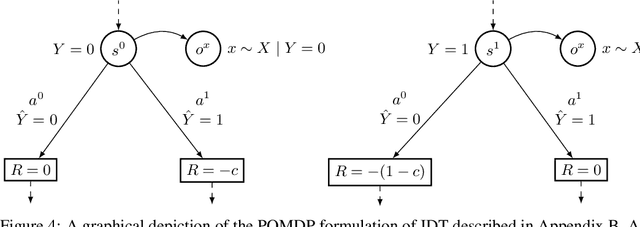
Existing observational approaches for learning human preferences, such as inverse reinforcement learning, usually make strong assumptions about the observability of the human's environment. However, in reality, people make many important decisions under uncertainty. To better understand preference learning in these cases, we study the setting of inverse decision theory (IDT), a previously proposed framework where a human is observed making non-sequential binary decisions under uncertainty. In IDT, the human's preferences are conveyed through their loss function, which expresses a tradeoff between different types of mistakes. We give the first statistical analysis of IDT, providing conditions necessary to identify these preferences and characterizing the sample complexity -- the number of decisions that must be observed to learn the tradeoff the human is making to a desired precision. Interestingly, we show that it is actually easier to identify preferences when the decision problem is more uncertain. Furthermore, uncertain decision problems allow us to relax the unrealistic assumption that the human is an optimal decision maker but still identify their exact preferences; we give sample complexities in this suboptimal case as well. Our analysis contradicts the intuition that partial observability should make preference learning more difficult. It also provides a first step towards understanding and improving preference learning methods for uncertain and suboptimal humans.