Learning Sparse Nonlinear Dynamics via Mixed-Integer Optimization
Paper and Code
Jun 01, 2022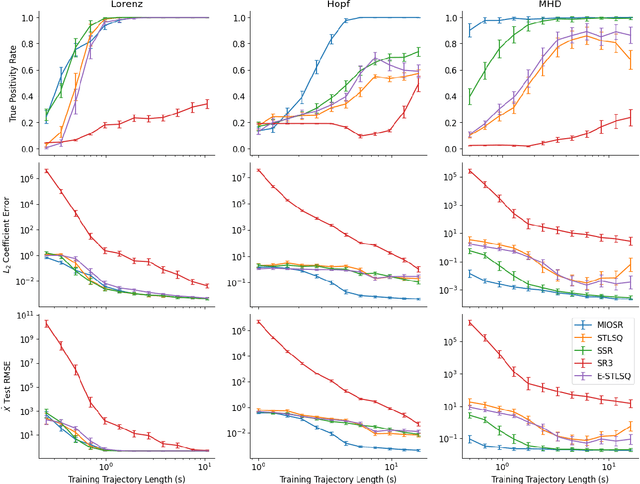
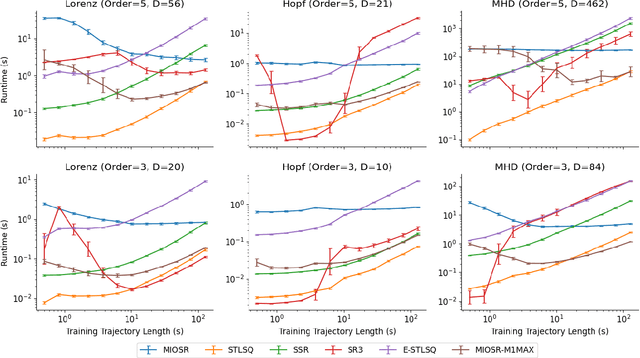
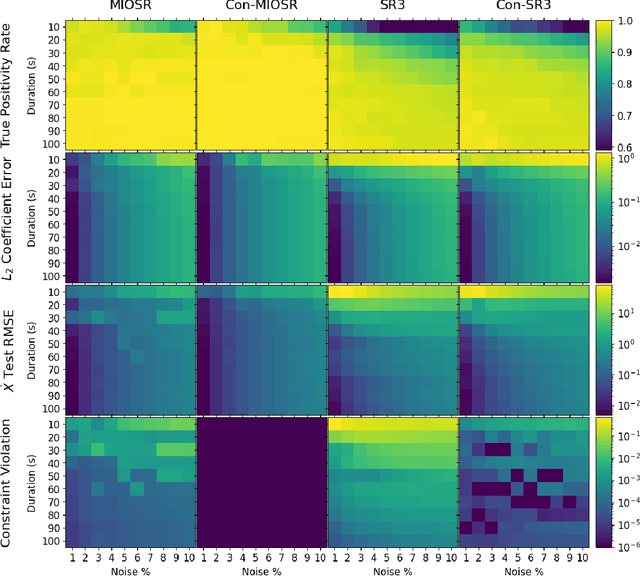
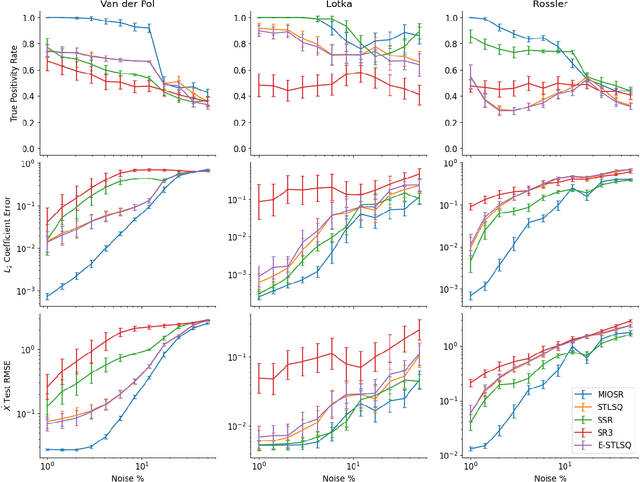
Discovering governing equations of complex dynamical systems directly from data is a central problem in scientific machine learning. In recent years, the sparse identification of nonlinear dynamics (SINDy) framework, powered by heuristic sparse regression methods, has become a dominant tool for learning parsimonious models. We propose an exact formulation of the SINDy problem using mixed-integer optimization (MIO) to solve the sparsity constrained regression problem to provable optimality in seconds. On a large number of canonical ordinary and partial differential equations, we illustrate the dramatic improvement of our approach in accurate model discovery while being more sample efficient, robust to noise, and flexible in accommodating physical constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge