Learning Smooth Representation for Unsupervised Domain Adaptation

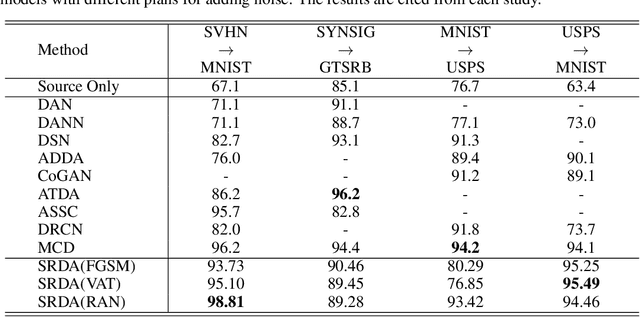
In unsupervised domain adaptation, existing methods utilizing the boundary decision have achieved remarkable performance, but they lack analysis of the relationship between decision boundary and features. In our work, we propose a new principle that adaptive classifiers and transferable features can be obtained in the target domain by learning smooth representations. We analyze the relationship between decision boundary and ambiguous target features in terms of smoothness. Thereafter, local smooth discrepancy is defined to measure the smoothness of a sample and detect sensitive samples which are easily misclassified. To strengthen the smoothness, sensitive samples are corrected in feature space by optimizing local smooth discrepancy. Moreover, the generalization error upper bound is derived theoretically. Finally, We evaluate our method in several standard benchmark datasets. Empirical evidence shows that the proposed method is comparable or superior to the state-of-the-art methods and local smooth discrepancy is a valid metric to evaluate the performance of a domain adaptation method.