Learning Self-Game-Play Agents for Combinatorial Optimization Problems
Paper and Code
Mar 08, 2019
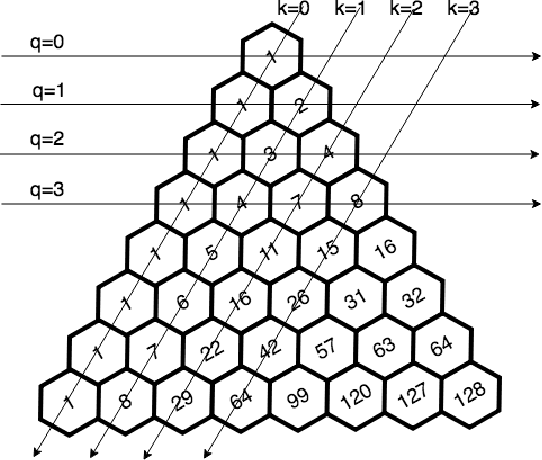
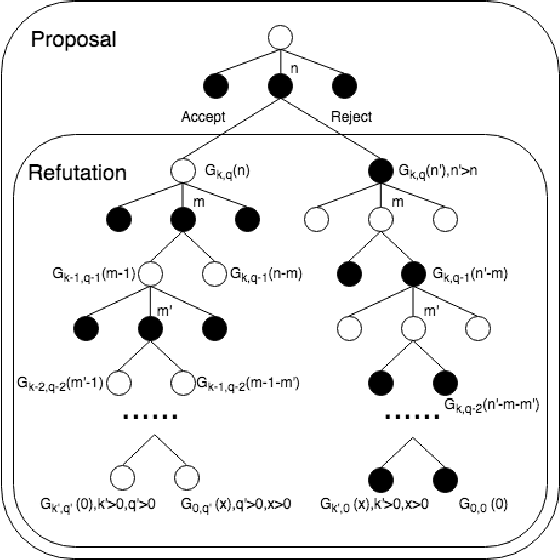

Recent progress in reinforcement learning (RL) using self-game-play has shown remarkable performance on several board games (e.g., Chess and Go) as well as video games (e.g., Atari games and Dota2). It is plausible to consider that RL, starting from zero knowledge, might be able to gradually approximate a winning strategy after a certain amount of training. In this paper, we explore neural Monte-Carlo-Tree-Search (neural MCTS), an RL algorithm which has been applied successfully by DeepMind to play Go and Chess at a super-human level. We try to leverage the computational power of neural MCTS to solve a class of combinatorial optimization problems. Following the idea of Hintikka's Game-Theoretical Semantics, we propose the Zermelo Gamification (ZG) to transform specific combinatorial optimization problems into Zermelo games whose winning strategies correspond to the solutions of the original optimization problem. The ZG also provides a specially designed neural MCTS. We use a combinatorial planning problem for which the ground-truth policy is efficiently computable to demonstrate that ZG is promising.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge