Learning Representations for Neural Network-Based Classification Using the Information Bottleneck Principle

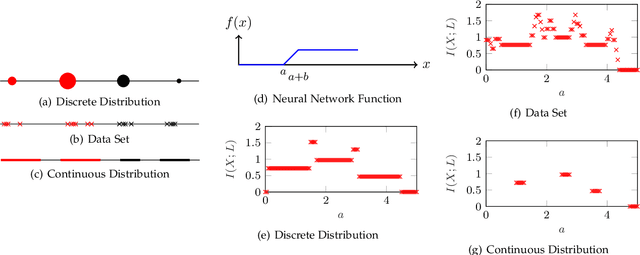
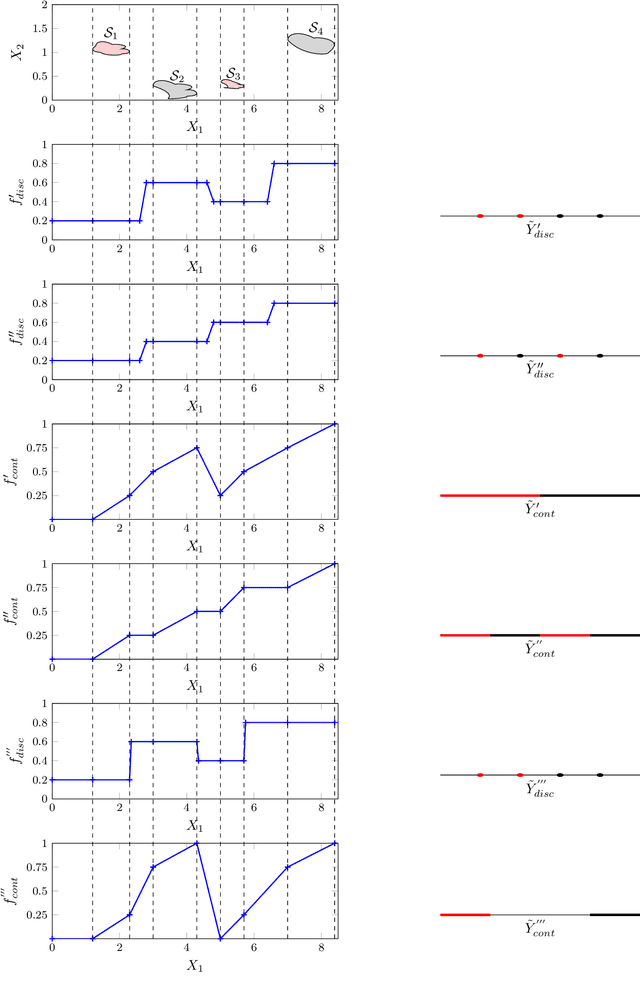
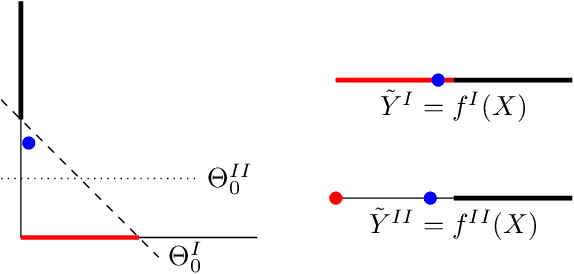
In this theory paper, we investigate training deep neural networks (DNNs) for classification via minimizing the information bottleneck (IB) functional. We show that the resulting optimization problem suffers from two severe issues: First, for deterministic DNNs, either the IB functional is infinite for almost all values of network parameters, making the optimization problem ill-posed, or it is piecewise constant, hence not admitting gradient-based optimization methods. Second, the invariance of the IB functional under bijections prevents it from capturing desirable properties for classification, such as robustness, architectural simplicity, and simplicity of the learned representation. We argue that these issues are partly resolved for stochastic DNNs, DNNs that include a (hard or soft) decision rule, or by replacing the IB functional with related, but more well-behaved cost functions. We conclude that recent successes reported about training DNNs using the IB framework must be attributed to such solutions. As a side effect, our results imply limitations of the IB framework for the analysis of DNNs. We also note that rather than trying to repair the inherent problems in IB functional, a better approach may be to design regularizers on latent representation enforcing the desired properties directly.