Learning Random Fourier Features by Hybrid Constrained Optimization
Paper and Code
Dec 07, 2017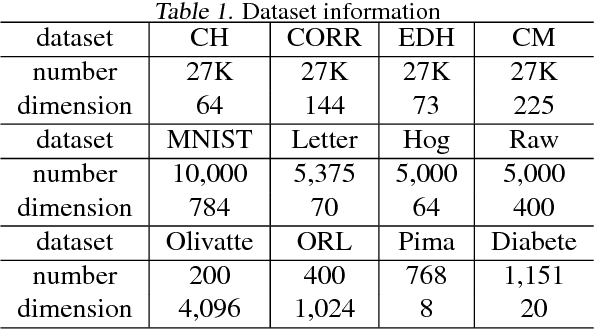
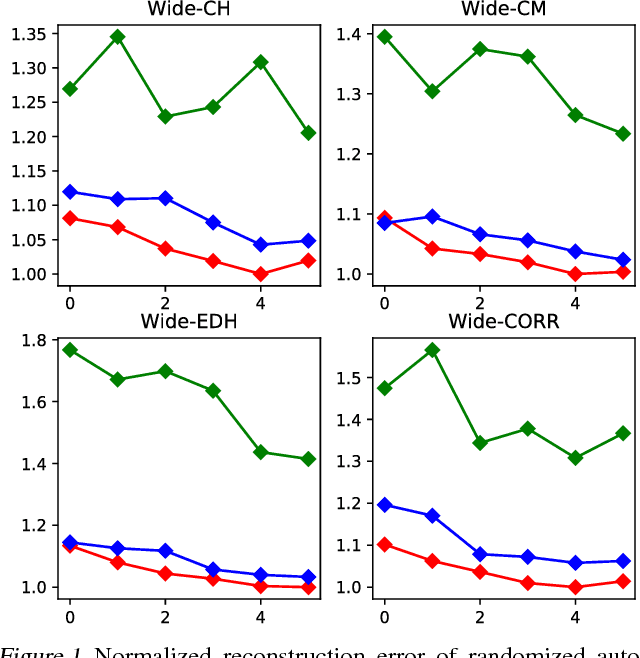
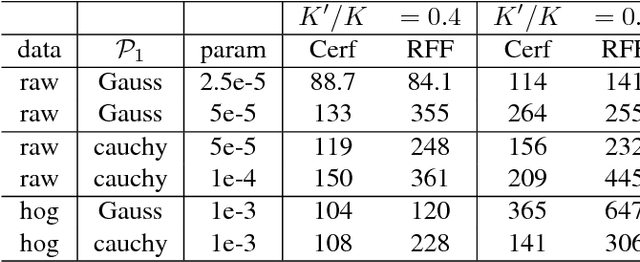
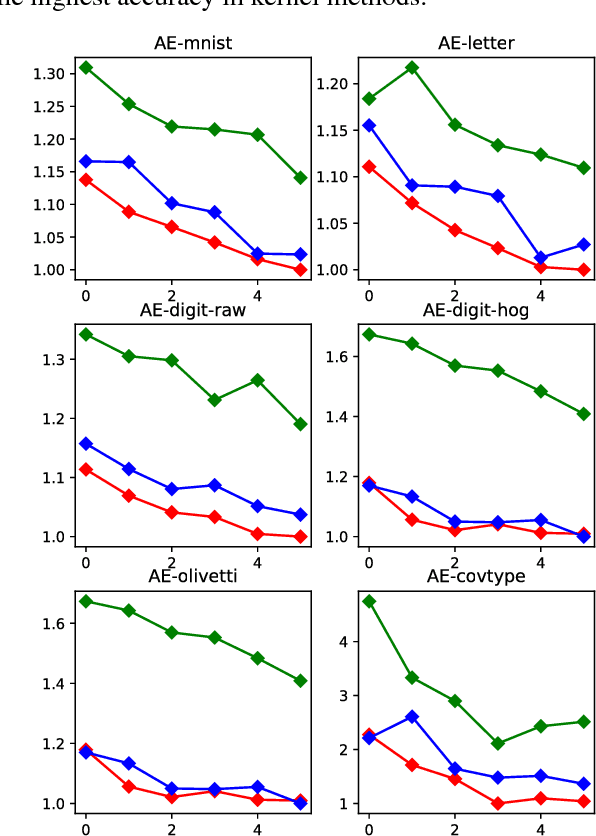
The kernel embedding algorithm is an important component for adapting kernel methods to large datasets. Since the algorithm consumes a major computation cost in the testing phase, we propose a novel teacher-learner framework of learning computation-efficient kernel embeddings from specific data. In the framework, the high-precision embeddings (teacher) transfer the data information to the computation-efficient kernel embeddings (learner). We jointly select informative embedding functions and pursue an orthogonal transformation between two embeddings. We propose a novel approach of constrained variational expectation maximization (CVEM), where the alternate direction method of multiplier (ADMM) is applied over a nonconvex domain in the maximization step. We also propose two specific formulations based on the prevalent Random Fourier Feature (RFF), the masked and blocked version of Computation-Efficient RFF (CERF), by imposing a random binary mask or a block structure on the transformation matrix. By empirical studies of several applications on different real-world datasets, we demonstrate that the CERF significantly improves the performance of kernel methods upon the RFF, under certain arithmetic operation requirements, and suitable for structured matrix multiplication in Fastfood type algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge