Learning Posterior and Prior for Uncertainty Modeling in Person Re-Identification
Paper and Code
Jul 17, 2020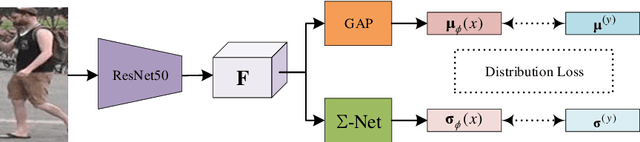
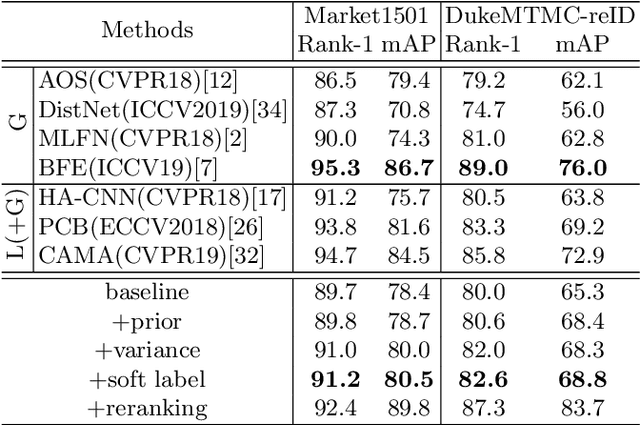
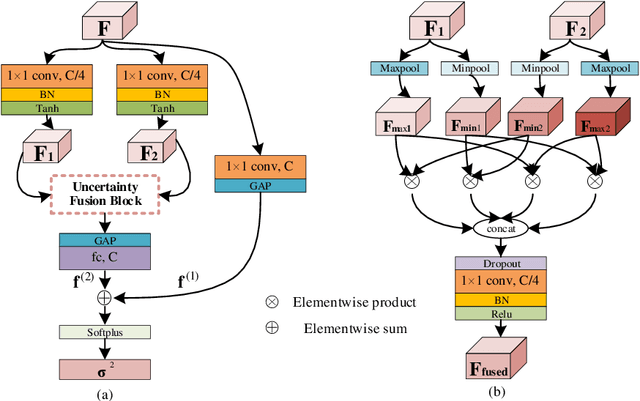
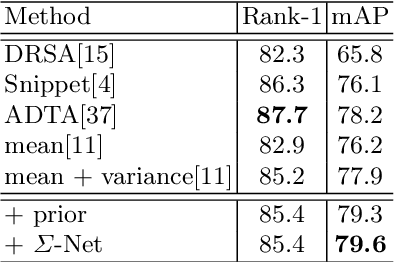
Data uncertainty in practical person reID is ubiquitous, hence it requires not only learning the discriminative features, but also modeling the uncertainty based on the input. This paper proposes to learn the sample posterior and the class prior distribution in the latent space, so that not only representative features but also the uncertainty can be built by the model. The prior reflects the distribution of all data in the same class, and it is the trainable model parameters. While the posterior is the probability density of a single sample, so it is actually the feature defined on the input. We assume that both of them are in Gaussian form. To simultaneously model them, we put forward a distribution loss, which measures the KL divergence from the posterior to the priors in the manner of supervised learning. In addition, we assume that the posterior variance, which is essentially the uncertainty, is supposed to have the second-order characteristic. Therefore, a $\Sigma-$net is proposed to compute it by the high order representation from its input. Extensive experiments have been carried out on Market1501, DukeMTMC, MARS and noisy dataset as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge