Learning One-hidden-layer neural networks via Provable Gradient Descent with Random Initialization
Paper and Code
Jul 16, 2019
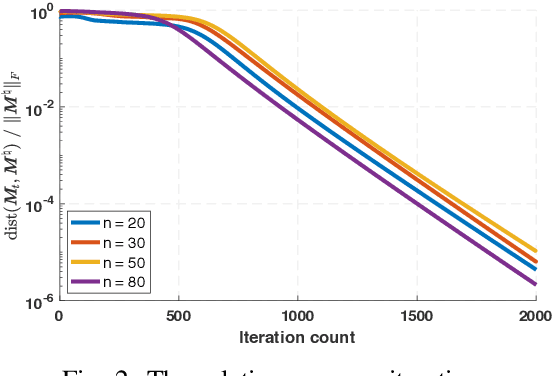


Although deep learning has shown its powerful performance in many applications, the mathematical principles behind neural networks are still mysterious. In this paper, we consider the problem of learning a one-hidden-layer neural network with quadratic activations. We focus on the under-parameterized regime where the number of hidden units is smaller than the dimension of the inputs. We shall propose to solve the problem via a provable gradient-based method with random initialization. For the non-convex neural networks training problem we reveal that the gradient descent iterates are able to enter a local region that enjoys strong convexity and smoothness within a few iterations, and then provably converges to a globally optimal model at a linear rate with near-optimal sample complexity. We further corroborate our theoretical findings via various experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge