Learning Multiple Belief Propagation Fixed Points for Real Time Inference
Paper and Code
Mar 27, 2009
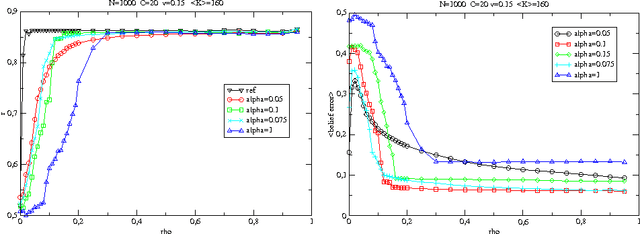

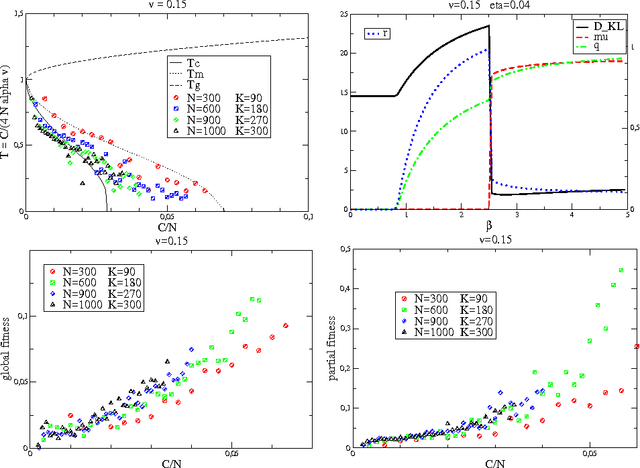
In the context of inference with expectation constraints, we propose an approach based on the "loopy belief propagation" algorithm LBP, as a surrogate to an exact Markov Random Field MRF modelling. A prior information composed of correlations among a large set of N variables, is encoded into a graphical model; this encoding is optimized with respect to an approximate decoding procedure LBP, which is used to infer hidden variables from an observed subset. We focus on the situation where the underlying data have many different statistical components, representing a variety of independent patterns. Considering a single parameter family of models we show how LBP may be used to encode and decode efficiently such information, without solving the NP hard inverse problem yielding the optimal MRF. Contrary to usual practice, we work in the non-convex Bethe free energy minimization framework, and manage to associate a belief propagation fixed point to each component of the underlying probabilistic mixture. The mean field limit is considered and yields an exact connection with the Hopfield model at finite temperature and steady state, when the number of mixture components is proportional to the number of variables. In addition, we provide an enhanced learning procedure, based on a straightforward multi-parameter extension of the model in conjunction with an effective continuous optimization procedure. This is performed using the stochastic search heuristic CMAES and yields a significant improvement with respect to the single parameter basic model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge