Learning many-body Hamiltonians with Heisenberg-limited scaling
Paper and Code
Oct 06, 2022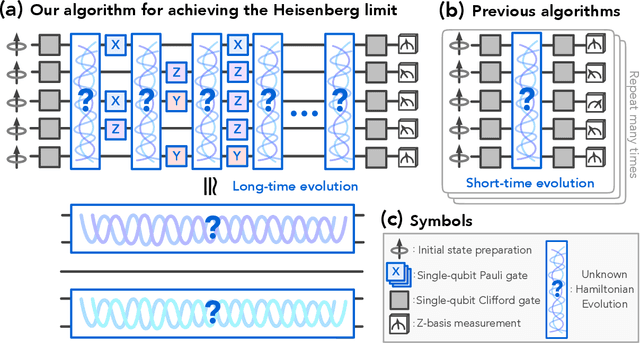
Learning a many-body Hamiltonian from its dynamics is a fundamental problem in physics. In this work, we propose the first algorithm to achieve the Heisenberg limit for learning an interacting $N$-qubit local Hamiltonian. After a total evolution time of $\mathcal{O}(\epsilon^{-1})$, the proposed algorithm can efficiently estimate any parameter in the $N$-qubit Hamiltonian to $\epsilon$-error with high probability. The proposed algorithm is robust against state preparation and measurement error, does not require eigenstates or thermal states, and only uses $\mathrm{polylog}(\epsilon^{-1})$ experiments. In contrast, the best previous algorithms, such as recent works using gradient-based optimization or polynomial interpolation, require a total evolution time of $\mathcal{O}(\epsilon^{-2})$ and $\mathcal{O}(\epsilon^{-2})$ experiments. Our algorithm uses ideas from quantum simulation to decouple the unknown $N$-qubit Hamiltonian $H$ into noninteracting patches, and learns $H$ using a quantum-enhanced divide-and-conquer approach. We prove a matching lower bound to establish the asymptotic optimality of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge