Learning low-precision neural networks without Straight-Through Estimator(STE)
Paper and Code
Mar 04, 2019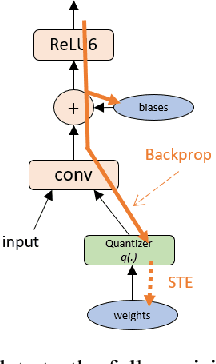
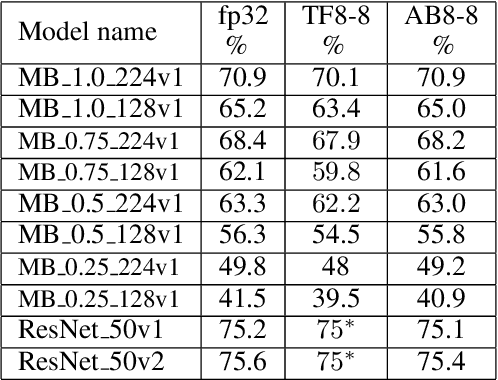
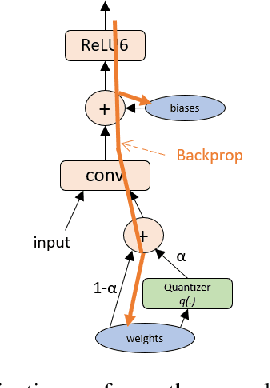
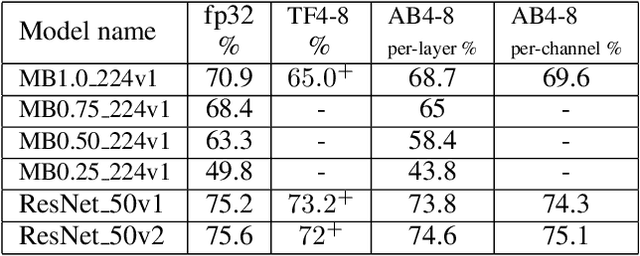
The Straight-Through Estimator (STE) is widely used for back-propagating gradients through the quantization function, but the STE technique lacks a complete theoretical understanding. We propose an alternative methodology called alpha-blending (AB), which quantizes neural networks to low-precision using stochastic gradient descent (SGD). Our method (AB) avoids STE approximation by replacing the quantized weight in the loss function by an affine combination of the quantized weight w_q and the corresponding full-precision weight w with non-trainable scalar coefficient $\alpha$ and $1-\alpha$. During training, $\alpha$ is gradually increased from 0 to 1; the gradient updates to the weights are through the full-precision term, $(1-\alpha)w$, of the affine combination; the model is converted from full-precision to low-precision progressively. To evaluate the method, a 1-bit BinaryNet on CIFAR10 dataset and 8-bits, 4-bits MobileNet v1, ResNet_50 v1/2 on ImageNet dataset are trained using the alpha-blending approach, and the evaluation indicates that AB improves top-1 accuracy by 0.9%, 0.82% and 2.93% respectively compared to the results of STE based quantization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge