Learning Linear Temporal Properties
Paper and Code
Sep 20, 2018
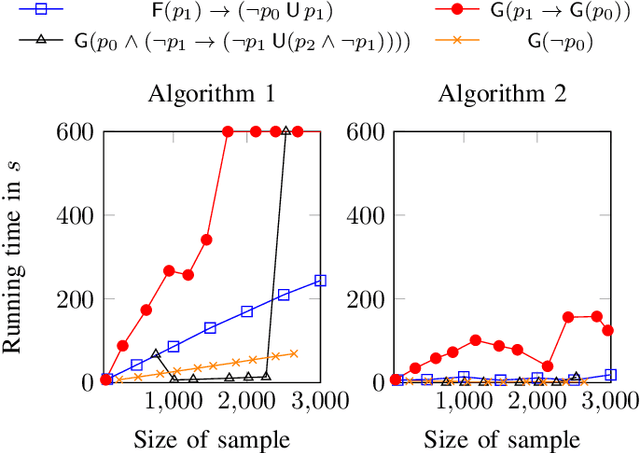
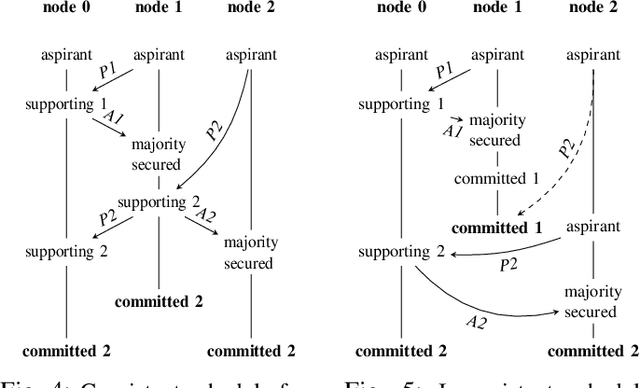
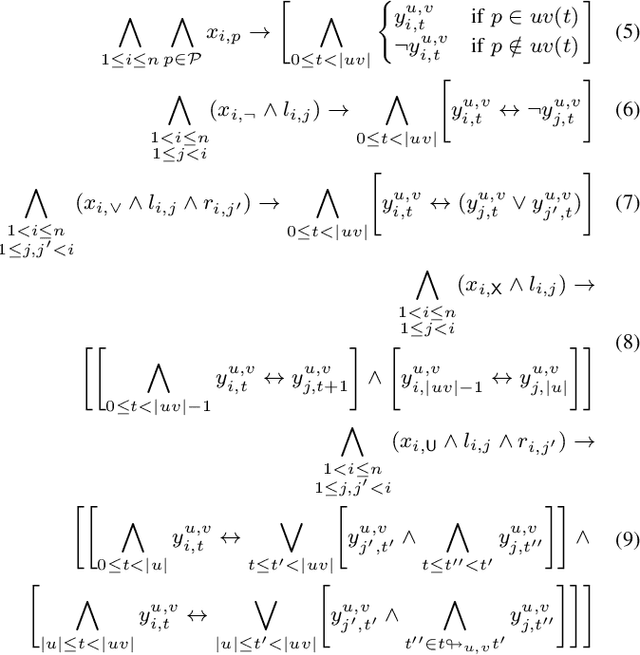
We present two novel algorithms for learning formulas in Linear Temporal Logic (LTL) from examples. The first learning algorithm reduces the learning task to a series of satisfiability problems in propositional Boolean logic and produces a smallest LTL formula (in terms of the number of subformulas) that is consistent with the given data. Our second learning algorithm, on the other hand, combines the SAT-based learning algorithm with classical algorithms for learning decision trees. The result is a learning algorithm that scales to real-world scenarios with hundreds of examples, but can no longer guarantee to produce minimal consistent LTL formulas. We compare both learning algorithms and demonstrate their performance on a wide range of synthetic benchmarks. Additionally, we illustrate their usefulness on the task of understanding executions of a leader election protocol.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge