Learning Latent Spaces for Domain Generalization in Time Series Forecasting

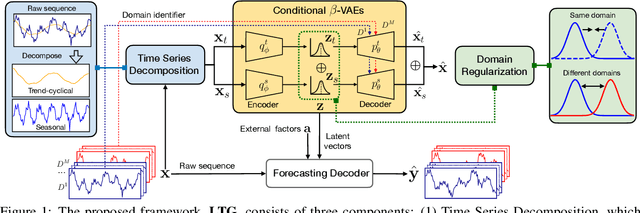
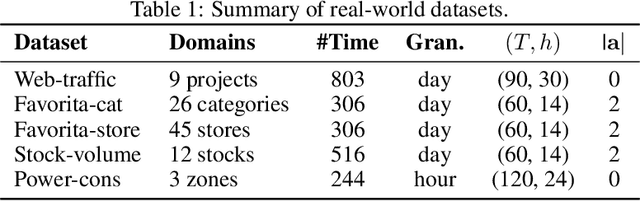
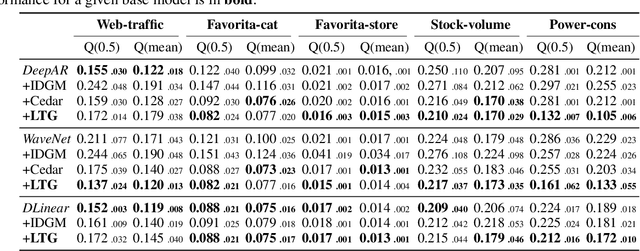
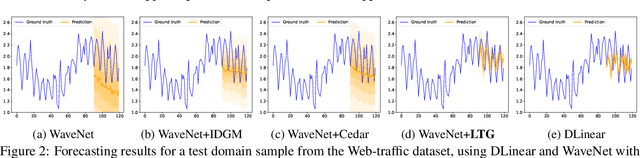
Time series forecasting is vital in many real-world applications, yet developing models that generalize well on unseen relevant domains -- such as forecasting web traffic data on new platforms/websites or estimating e-commerce demand in new regions -- remains underexplored. Existing forecasting models often struggle with domain shifts in time series data, as the temporal patterns involve complex components like trends, seasonality, etc. While some prior work addresses this by matching feature distributions across domains or disentangling domain-shared features using label information, they fail to reveal insights into the latent temporal dependencies, which are critical for identifying common patterns across domains and achieving generalization. We propose a framework for domain generalization in time series forecasting by mining the latent factors that govern temporal dependencies across domains. Our approach uses a decomposition-based architecture with a new Conditional $\beta$-Variational Autoencoder (VAE), wherein time series data is first decomposed into trend-cyclical and seasonal components, each modeled independently through separate $\beta$-VAE modules. The $\beta$-VAE aims to capture disentangled latent factors that control temporal dependencies across domains. We enhance the learning of domain-specific information with a decoder-conditional design and introduce domain regularization to improve the separation of domain-shared and domain-specific latent factors. Our proposed method is flexible and can be applied to various time series forecasting models, enabling effective domain generalization with simplicity and efficiency. We validate its effectiveness on five real-world time series datasets, covering web traffic, e-commerce, finance and power consumption, demonstrating improved generalization performance over state-of-the-art methods.