Learning Invariant Representations for Equivariant Neural Networks Using Orthogonal Moments
Paper and Code
Sep 22, 2022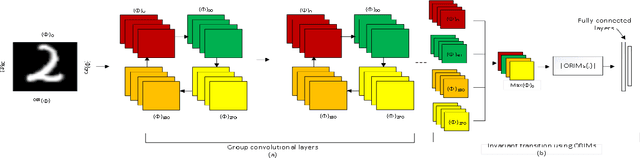
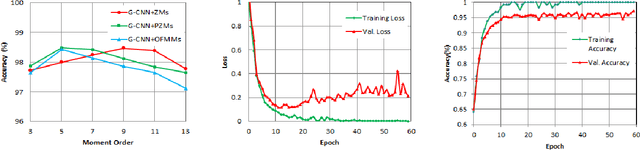


The convolutional layers of standard convolutional neural networks (CNNs) are equivariant to translation. However, the convolution and fully-connected layers are not equivariant or invariant to other affine geometric transformations. Recently, a new class of CNNs is proposed in which the conventional layers of CNNs are replaced with equivariant convolution, pooling, and batch-normalization layers. The final classification layer in equivariant neural networks is invariant to different affine geometric transformations such as rotation, reflection and translation, and the scalar value is obtained by either eliminating the spatial dimensions of filter responses using convolution and down-sampling throughout the network or average is taken over the filter responses. In this work, we propose to integrate the orthogonal moments which gives the high-order statistics of the function as an effective means for encoding global invariance with respect to rotation, reflection and translation in fully-connected layers. As a result, the intermediate layers of the network become equivariant while the classification layer becomes invariant. The most widely used Zernike, pseudo-Zernike and orthogonal Fourier-Mellin moments are considered for this purpose. The effectiveness of the proposed work is evaluated by integrating the invariant transition and fully-connected layer in the architecture of group-equivariant CNNs (G-CNNs) on rotated MNIST and CIFAR10 datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge