Learning Independently-Obtainable Reward Functions
Paper and Code
Jan 31, 2019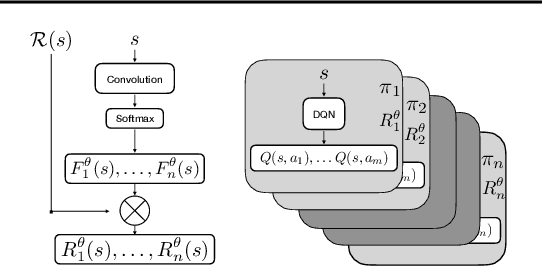
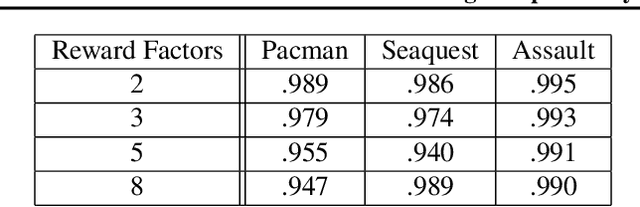
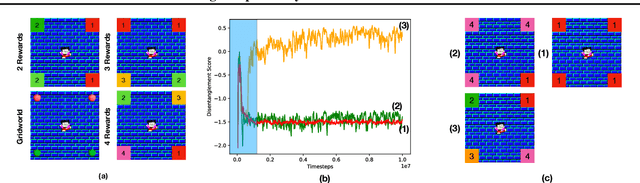
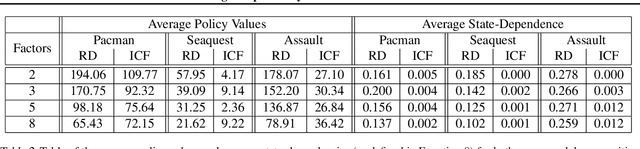
We present a novel method for learning a set of disentangled reward functions that sum to the original environment reward and are constrained to be independently obtainable. We define independent obtainability in terms of value functions with respect to obtaining one learned reward while pursuing another learned reward. Empirically, we illustrate that our method can learn meaningful reward decompositions in a variety of domains and that these decompositions exhibit some form of generalization performance when the environment's reward is modified. Theoretically, we derive results about the effect of maximizing our method's objective on the resulting reward functions and their corresponding optimal policies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge