Learning in Markov Games with Adaptive Adversaries: Policy Regret, Fundamental Barriers, and Efficient Algorithms
Paper and Code
Nov 01, 2024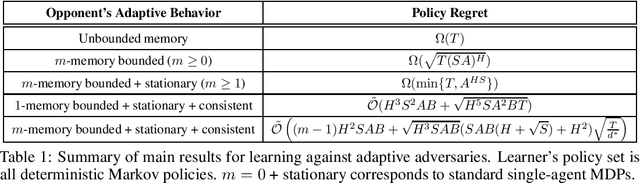
We study learning in a dynamically evolving environment modeled as a Markov game between a learner and a strategic opponent that can adapt to the learner's strategies. While most existing works in Markov games focus on external regret as the learning objective, external regret becomes inadequate when the adversaries are adaptive. In this work, we focus on \emph{policy regret} -- a counterfactual notion that aims to compete with the return that would have been attained if the learner had followed the best fixed sequence of policy, in hindsight. We show that if the opponent has unbounded memory or if it is non-stationary, then sample-efficient learning is not possible. For memory-bounded and stationary, we show that learning is still statistically hard if the set of feasible strategies for the learner is exponentially large. To guarantee learnability, we introduce a new notion of \emph{consistent} adaptive adversaries, wherein, the adversary responds similarly to similar strategies of the learner. We provide algorithms that achieve $\sqrt{T}$ policy regret against memory-bounded, stationary, and consistent adversaries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge