Learning from graphs with structural variation
Paper and Code
Jun 29, 2018
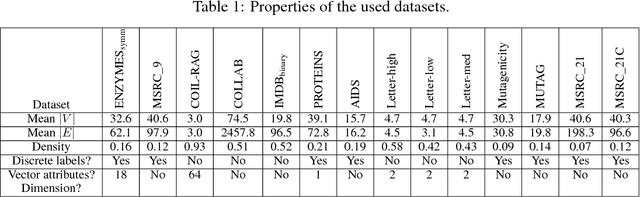
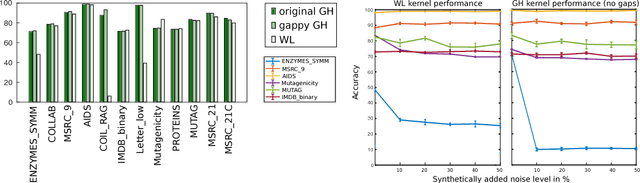
We study the effect of structural variation in graph data on the predictive performance of graph kernels. To this end, we introduce a novel, noise-robust adaptation of the GraphHopper kernel and validate it on benchmark data, obtaining modestly improved predictive performance on a range of datasets. Next, we investigate the performance of the state-of-the-art Weisfeiler-Lehman graph kernel under increasing synthetic structural errors and find that the effect of introducing errors depends strongly on the dataset.
* Presented at the NIPS 2017 workshop "Learning on Distributions,
Functions, Graphs and Groups"
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge