Learning directed acyclic graphs via bootstrap aggregating
Paper and Code
Jun 09, 2014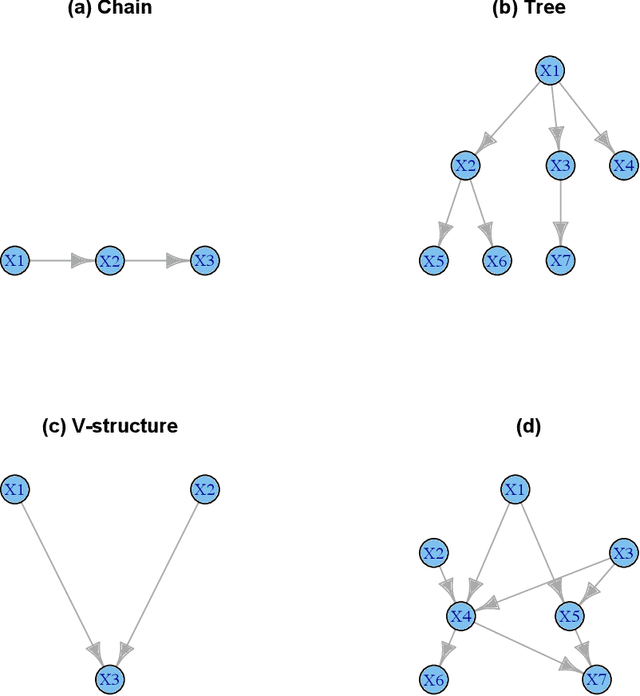
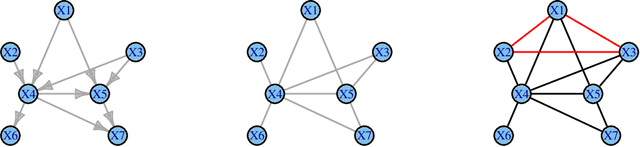


Probabilistic graphical models are graphical representations of probability distributions. Graphical models have applications in many fields including biology, social sciences, linguistic, neuroscience. In this paper, we propose directed acyclic graphs (DAGs) learning via bootstrap aggregating. The proposed procedure is named as DAGBag. Specifically, an ensemble of DAGs is first learned based on bootstrap resamples of the data and then an aggregated DAG is derived by minimizing the overall distance to the entire ensemble. A family of metrics based on the structural hamming distance is defined for the space of DAGs (of a given node set) and is used for aggregation. Under the high-dimensional-low-sample size setting, the graph learned on one data set often has excessive number of false positive edges due to over-fitting of the noise. Aggregation overcomes over-fitting through variance reduction and thus greatly reduces false positives. We also develop an efficient implementation of the hill climbing search algorithm of DAG learning which makes the proposed method computationally competitive for the high-dimensional regime. The DAGBag procedure is implemented in the R package dagbag.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge