Learning causal effects from many randomized experiments using regularized instrumental variables
Paper and Code
Jun 01, 2017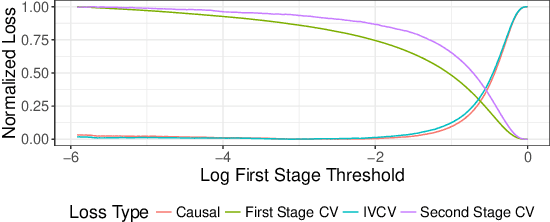
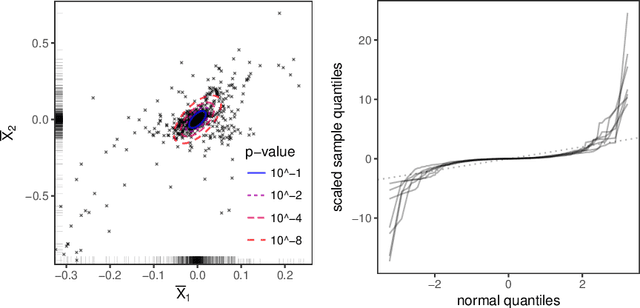
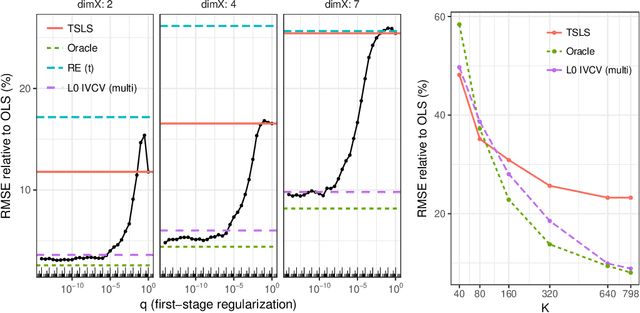
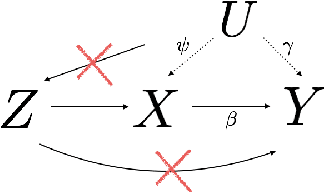
Scientific and business practices are increasingly resulting in large collections of randomized experiments. Analyzed together, these collections can tell us things that individual experiments in the collection cannot. We study how to learn causal relationships between variables from the kinds of collections faced by modern data scientists: the number of experiments is large, many experiments have very small effects, and the analyst lacks metadata (e.g., descriptions of the interventions). Here we use experimental groups as instrumental variables (IV) and show that a standard method (two-stage least squares) is biased even when the number of experiments is infinite. We show how a sparsity-inducing l0 regularization can --- in a reversal of the standard bias--variance tradeoff in regularization --- reduce bias (and thus error) of interventional predictions. Because we are interested in interventional loss minimization we also propose a modified cross-validation procedure (IVCV) to feasibly select the regularization parameter. We show, using a trick from Monte Carlo sampling, that IVCV can be done using summary statistics instead of raw data. This makes our full procedure simple to use in many real-world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge