Learn the Manipulation of Deformable Objects Using Tangent Space Point Set Registration
Paper and Code
Oct 09, 2018
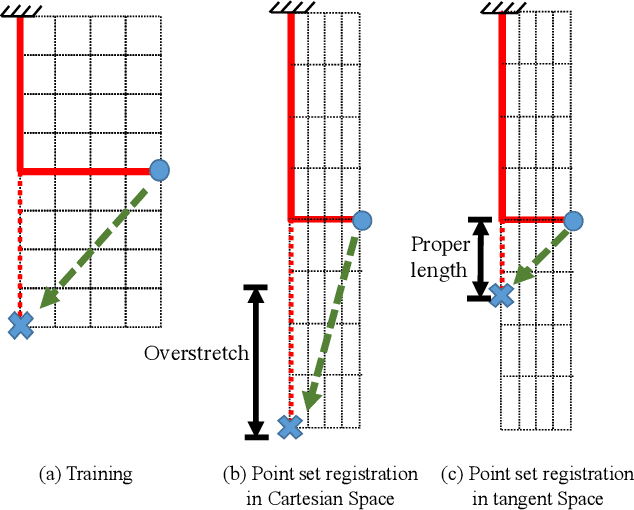
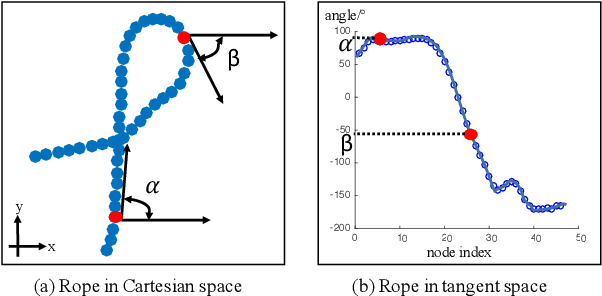
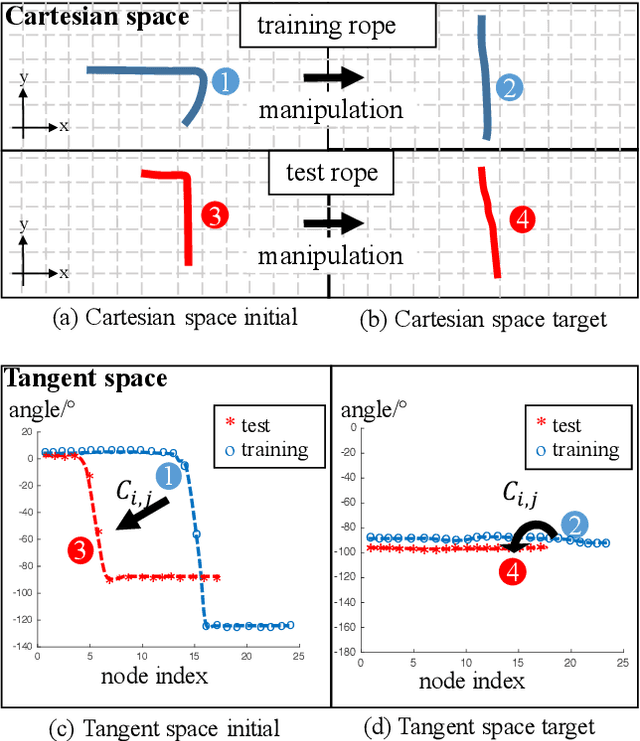
Point set registration is a powerful method that enables robots to manipulate deformable objects. By mapping the point cloud of the current object to the pre-trained point cloud, a transformation function can be constructed. The manipulator's trajectory for pre-trained shapes can be warped with this transformation function, yielding a feasible trajectory for the new shape. However, usually this transformation function regards objects as discrete points, and dismisses the topological structures. Therefore, it risks over-stretching or over-compression during manipulation. To tackle this problem, this paper proposes a tangent space point set registration method. A tangent space representation of an object is constructed by defining an angle for each node on the object. Point set registration algorithm runs in this newly-constructed tangent space, yielding a tangent space trajectory. The trajectory is then converted back to Cartesian space and carried out by the robot. Compared to its counterpart in Cartesian space, tangent space point set registration is safer and more robust, succeeding in a series of experiments such as rope straightening, rope knotting, cloth folding and unfolding.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge