LeapsAndBounds: A Method for Approximately Optimal Algorithm Configuration
Paper and Code
Jul 02, 2018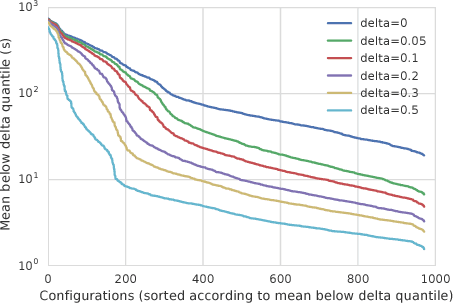
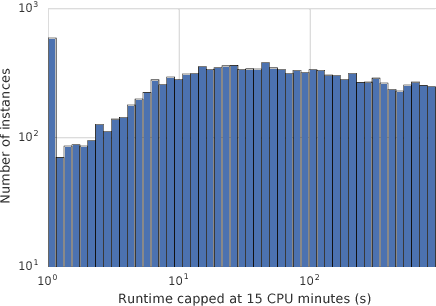
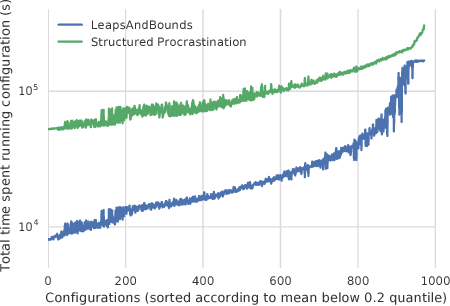
We consider the problem of configuring general-purpose solvers to run efficiently on problem instances drawn from an unknown distribution. The goal of the configurator is to find a configuration that runs fast on average on most instances, and do so with the least amount of total work. It can run a chosen solver on a random instance until the solver finishes or a timeout is reached. We propose LeapsAndBounds, an algorithm that tests configurations on randomly selected problem instances for longer and longer time. We prove that the capped expected runtime of the configuration returned by LeapsAndBounds is close to the optimal expected runtime, while our algorithm's running time is near-optimal. Our results show that LeapsAndBounds is more efficient than the recent algorithm of Kleinberg et al. (2017), which, to our knowledge, is the only other algorithm configuration method with non-trivial theoretical guarantees. Experimental results on configuring a public SAT solver on a new benchmark dataset also stand witness to the superiority of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge