Lazy Receding Horizon A* for Efficient Path Planning in Graphs with Expensive-to-Evaluate Edges
Paper and Code
Mar 15, 2018

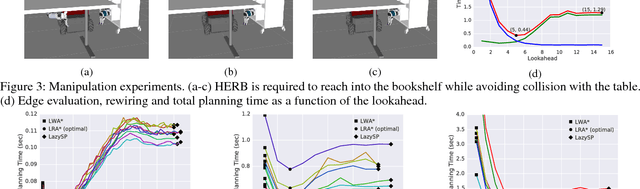

Motion-planning problems, such as manipulation in cluttered environments, often require a collision-free shortest path to be computed quickly given a roadmap graph. Typically, the computational cost of evaluating whether an edge of the roadmap graph is collision-free dominates the running time of search algorithms. Algorithms such as Lazy Weighted A* (LWA*) and LazySP have been proposed to reduce the number of edge evaluations by employing a lazy lookahead (one-step lookahead and infinite-step lookahead, respectively). However, this comes at the expense of additional graph operations: the larger the lookahead, the more the graph operations that are typically required. We propose Lazy Receding-Horizon A* (LRA*) to minimize the total planning time by balancing edge evaluations and graph operations. Endowed with a lazy lookahead, LRA* represents a family of lazy shortest-path graph-search algorithms that generalizes LWA* and LazySP. We analyze the theoretic properties of LRA* and demonstrate empirically that, in many cases, to minimize the total planning time, the algorithm requires an intermediate lazy lookahead. Namely, using an intermediate lazy lookahead, our algorithm outperforms both LWA* and LazySP. These experiments span simulated random worlds in $\mathbb{R}^2$ and $\mathbb{R}^4$, and manipulation problems using a 7-DOF manipulator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge