LassoBench: A High-Dimensional Hyperparameter Optimization Benchmark Suite for Lasso
Paper and Code
Nov 04, 2021
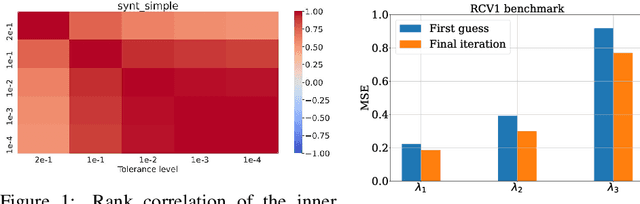

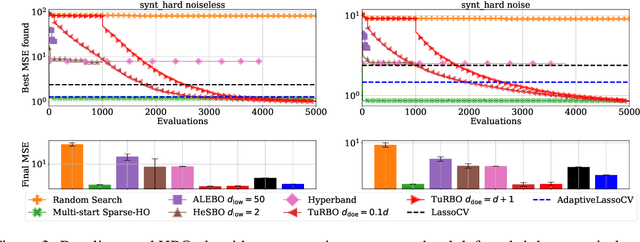
Even though Weighted Lasso regression has appealing statistical guarantees, it is typically avoided due to its complex search space described with thousands of hyperparameters. On the other hand, the latest progress with high-dimensional HPO methods for black-box functions demonstrates that high-dimensional applications can indeed be efficiently optimized. Despite this initial success, the high-dimensional HPO approaches are typically applied to synthetic problems with a moderate number of dimensions which limits its impact in scientific and engineering applications. To address this limitation, we propose LassoBench, a new benchmark suite tailored for an important open research topic in the Lasso community that is Weighted Lasso regression. LassoBench consists of benchmarks on both well-controlled synthetic setups (number of samples, SNR, ambient and effective dimensionalities, and multiple fidelities) and real-world datasets, which enable the use of many flavors of HPO algorithms to be improved and extended to the high-dimensional setting. We evaluate 5 state-of-the-art HPO methods and 3 baselines, and demonstrate that Bayesian optimization, in particular, can improve over the methods commonly used for sparse regression while highlighting limitations of these frameworks in very high-dimensions. Remarkably, Bayesian optimization improve the Lasso baselines on 60, 100, 300, and 1000 dimensional problems by 45.7%, 19.2%, 19.7% and 15.5%, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge