Lasso Guarantees for Time Series Estimation Under Subgaussian Tails and $ β$-Mixing

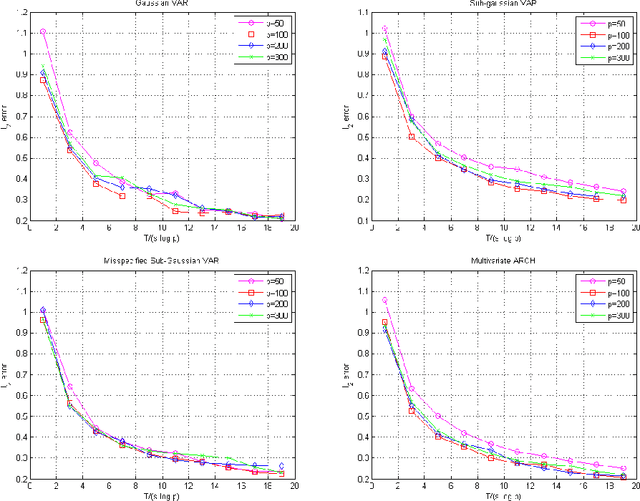
Many theoretical results on estimation of high dimensional time series require specifying an underlying data generating model (DGM). Instead, along the footsteps of~\cite{wong2017lasso}, this paper relies only on (strict) stationarity and $ \beta $-mixing condition to establish consistency of lasso when data comes from a $\beta$-mixing process with marginals having subgaussian tails. Because of the general assumptions, the data can come from DGMs different than standard time series models such as VAR or ARCH. When the true DGM is not VAR, the lasso estimates correspond to those of the best linear predictors using the past observations. We establish non-asymptotic inequalities for estimation and prediction errors of the lasso estimates. Together with~\cite{wong2017lasso}, we provide lasso guarantees that cover full spectrum of the parameters in specifications of $ \beta $-mixing subgaussian time series. Applications of these results potentially extend to non-Gaussian, non-Markovian and non-linear times series models as the examples we provide demonstrate. In order to prove our results, we derive a novel Hanson-Wright type concentration inequality for $\beta$-mixing subgaussian random vectors that may be of independent interest.