Large-scale nonlinear Granger causality: A data-driven, multivariate approach to recovering directed networks from short time-series data
Paper and Code
Sep 10, 2020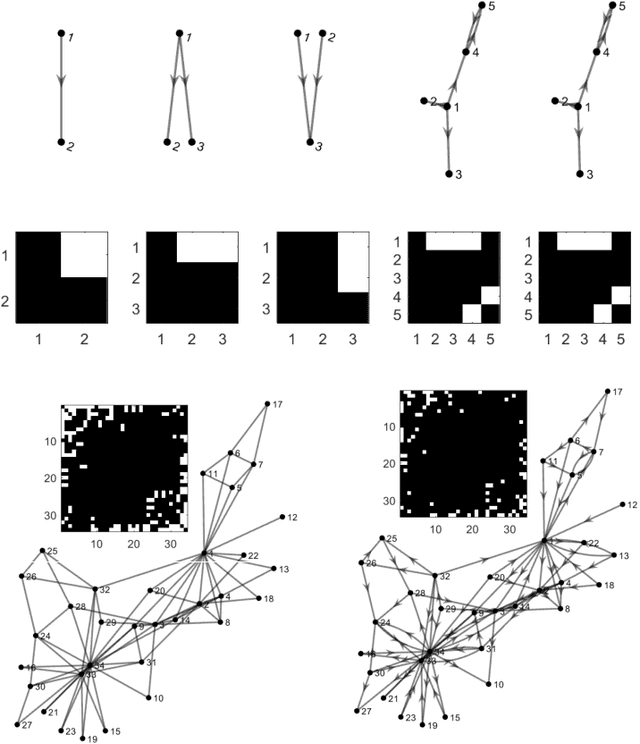
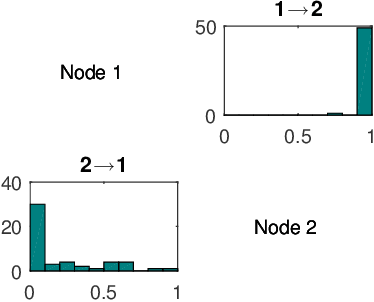
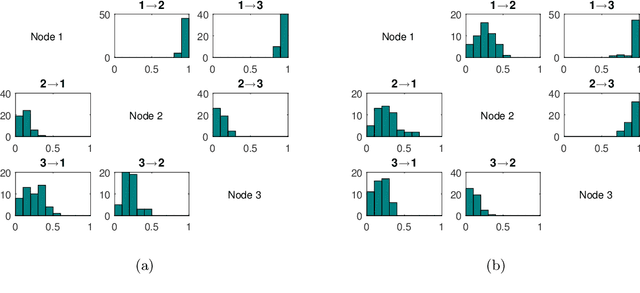
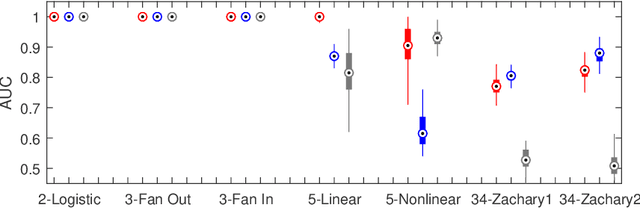
To gain insight into complex systems it is a key challenge to infer nonlinear causal directional relations from observational time-series data. Specifically, estimating causal relationships between interacting components in large systems with only short recordings over few temporal observations remains an important, yet unresolved problem. Here, we introduce a large-scale Nonlinear Granger Causality (lsNGC) approach for inferring directional, nonlinear, multivariate causal interactions between system components from short high-dimensional time-series recordings. By modeling interactions with nonlinear state-space transformations from limited observational data, lsNGC identifies casual relations with no explicit a priori assumptions on functional interdependence between component time-series in a computationally efficient manner. Additionally, our method provides a mathematical formulation revealing statistical significance of inferred causal relations. We extensively study the ability of lsNGC to recovering network structure from two-node to thirty-four node chaotic time-series systems. Our results suggest that lsNGC captures meaningful interactions from limited observational data, where it performs favorably when compared to traditionally used methods. Finally, we demonstrate the applicability of lsNGC to estimating causality in large, real-world systems by inferring directional nonlinear, multivariate causal relationships among a large number of relatively short time-series acquired from functional Magnetic Resonance Imaging (fMRI) data of the human brain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge