Large scale classification in deep neural network with Label Mapping
Paper and Code
Jun 07, 2018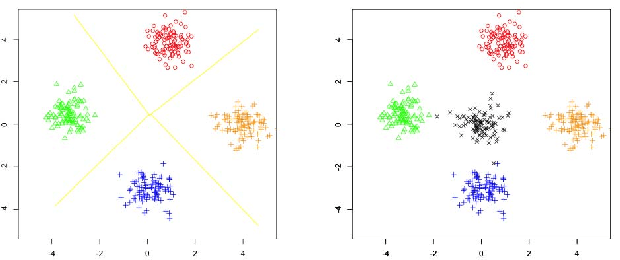
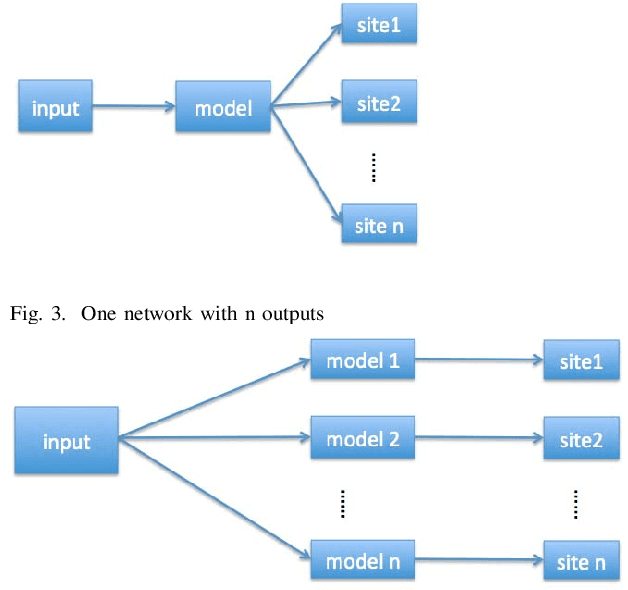
In recent years, deep neural network is widely used in machine learning. The multi-class classification problem is a class of important problem in machine learning. However, in order to solve those types of multi-class classification problems effectively, the required network size should have hyper-linear growth with respect to the number of classes. Therefore, it is infeasible to solve the multi-class classification problem using deep neural network when the number of classes are huge. This paper presents a method, so called Label Mapping (LM), to solve this problem by decomposing the original classification problem to several smaller sub-problems which are solvable theoretically. Our method is an ensemble method like error-correcting output codes (ECOC), but it allows base learners to be multi-class classifiers with different number of class labels. We propose two design principles for LM, one is to maximize the number of base classifier which can separate two different classes, and the other is to keep all base learners to be independent as possible in order to reduce the redundant information. Based on these principles, two different LM algorithms are derived using number theory and information theory. Since each base learner can be trained independently, it is easy to scale our method into a large scale training system. Experiments show that our proposed method outperforms the standard one-hot encoding and ECOC significantly in terms of accuracy and model complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge