Langevin Monte Carlo: random coordinate descent and variance reduction
Paper and Code
Jul 29, 2020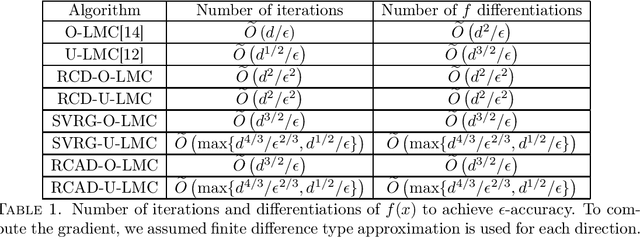
Sampling from a log-concave distribution function on $\mathbb{R}^d$ (with $d\gg 1$) is a popular problem that has wide applications. In this paper we study the application of random coordinate descent method (RCD) on the Langevin Monte Carlo (LMC) sampling method, and we find two sides of the theory: 1. The direct application of RCD on LMC does reduce the number of finite differencing approximations per iteration, but it induces a large variance error term. More iterations are then needed, and ultimately the method gains no computational advantage; 2. When variance reduction techniques (such as SAGA and SVRG) are incorporated in RCD-LMC, the variance error term is reduced. The new methods, compared to the vanilla LMC, reduce the total computational cost by $d$ folds, and achieve the optimal cost rate. We perform our investigations in both overdamped and underdamped settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge