kNN-Res: Residual Neural Network with kNN-Graph coherence for point cloud registration
Paper and Code
Mar 31, 2023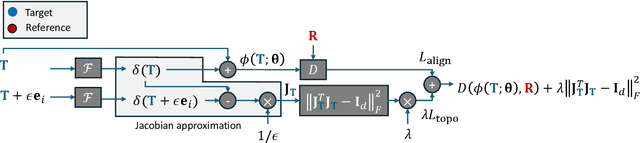
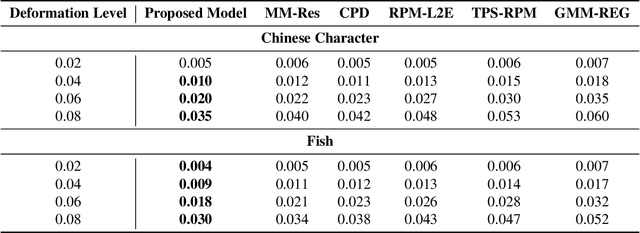
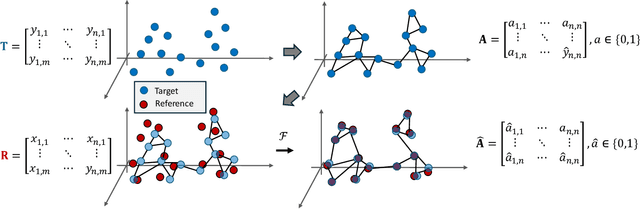
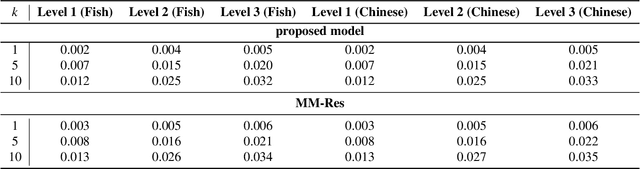
In this paper, we present a residual neural network-based method for point set registration. Given a target and a reference point cloud, the goal is to learn a minimal transformation that aligns the target to the reference under the constraint that the topological structure of the target point cloud is preserved. Similar to coherent point drift (CPD), the registration (alignment) problem is viewed as the movement of data points sampled from a target distribution along a regularized displacement vector field. While the coherence constraint in CPD is stated in terms of local motion coherence, the proposed regularization term relies on a global smoothness constraint as a proxy for preserving local topology. This makes CPD less flexible when the deformation is locally rigid but globally non-rigid as in the case of multiple objects and articulate pose registration. To mitigate these issues, a Jacobian-based cost function along with geometric-aware statistical distances is proposed. The latter allows for measuring misalignment between the target and the reference. The justification for the kNN-graph preservation of target data, when the Jacobian cost is used, is also provided. Further, a stochastic approximation for high dimensional registration is introduced to make a high-dimensional alignment feasible. The proposed method is tested on high-dimensional Flow Cytometry to align two data distributions whilst preserving the kNN-graph of the data. The implementation of the proposed approach is available at https://github.com/MuhammadSaeedBatikh/kNN-Res_Demo/ under the MIT license.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge