Kernels on fuzzy sets: an overview
Paper and Code
Jul 30, 2019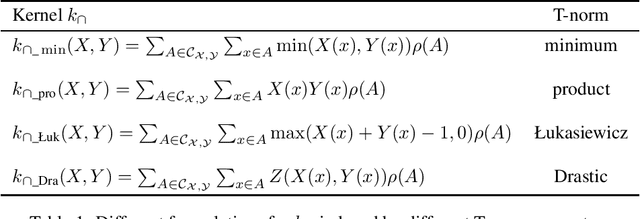
This paper introduces the concept of kernels on fuzzy sets as a similarity measure for $[0,1]$-valued functions, a.k.a. \emph{membership functions of fuzzy sets}. We defined the following classes of kernels: the cross product, the intersection, the non-singleton and the distance-based kernels on fuzzy sets. Applicability of those kernels are on machine learning and data science tasks where uncertainty in data has an ontic or epistemistic interpretation.
* Learning on Distributions, Functions, Graphs and Groups @ NIPS-2017,
8th Dec
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge