K-Receiver Wiretap Channel: Optimal Encoding Order and Signaling Design
Paper and Code
Jun 01, 2022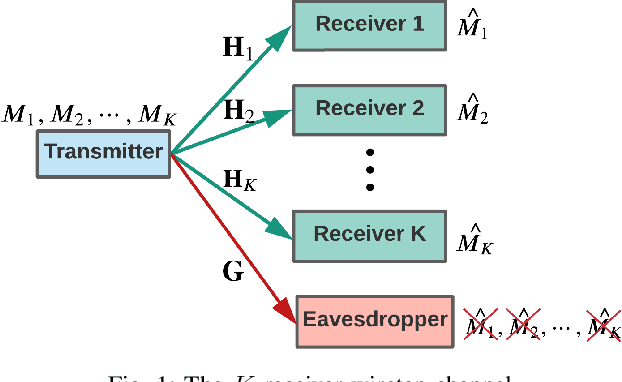
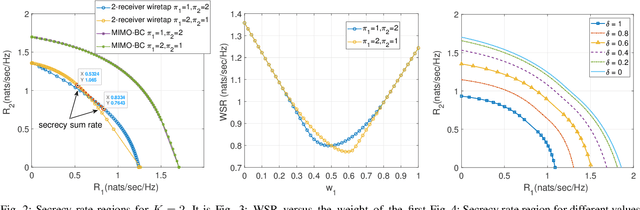
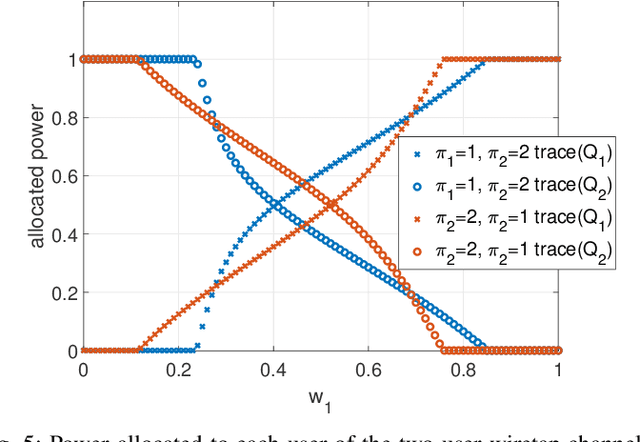
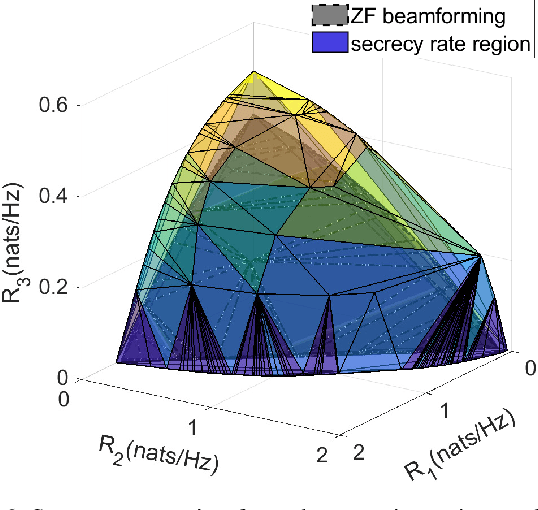
The K-receiver wiretap channel is a channel model where a transmitter broadcasts K independent messages to K intended receivers while keeping them secret from an eavesdropper. The capacity region of the K-receiver multiple-input multiple-output (MIMO) wiretap channel has been characterized by using dirty-paper coding and stochastic encoding. However, K factorial encoding orders may need to be enumerated to evaluate the capacity region, which makes the problem intractable. In addition, even though the capacity region is known, the optimal signaling to achieve the capacity region is unknown. In this paper, we determine one optimal encoding order to achieve every point on the capacity region, and thus reduce the encoding complexity K factorial times. We prove that the optimal decoding order for the K-receiver MIMO wiretap channel is the same as that for the MIMO broadcast channel without secrecy. To be specific, the descending weight ordering in the weighted sum-rate (WSR) maximization problem determines the optimal encoding order. Next, to reach the border of the secrecy capacity region, we form a WSR maximization problem and apply the block successive maximization method to solve this nonconvex problem and find the input covariance matrices corresponding to each message. Numerical results are used to verify the optimality of the encoding order and to demonstrate the efficacy of the proposed signaling design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge