JR-GAN: Jacobian Regularization for Generative Adversarial Networks
Paper and Code
Jun 24, 2018
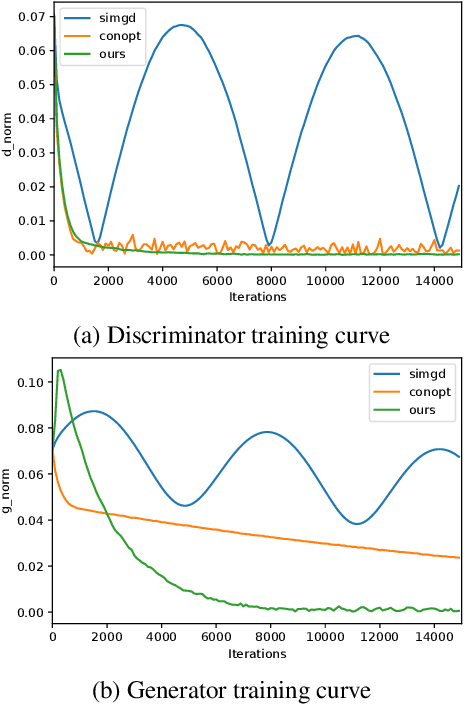
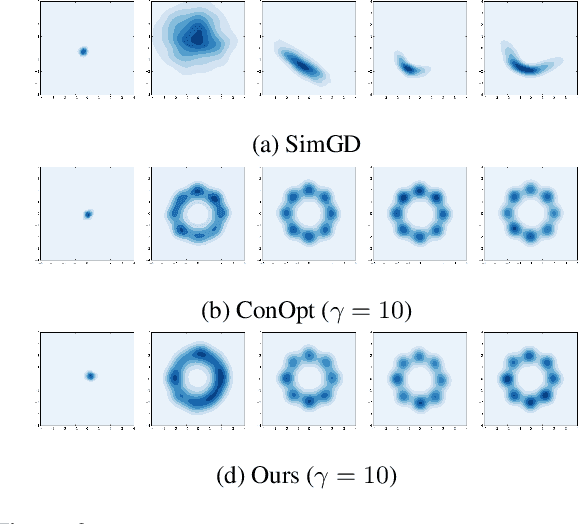
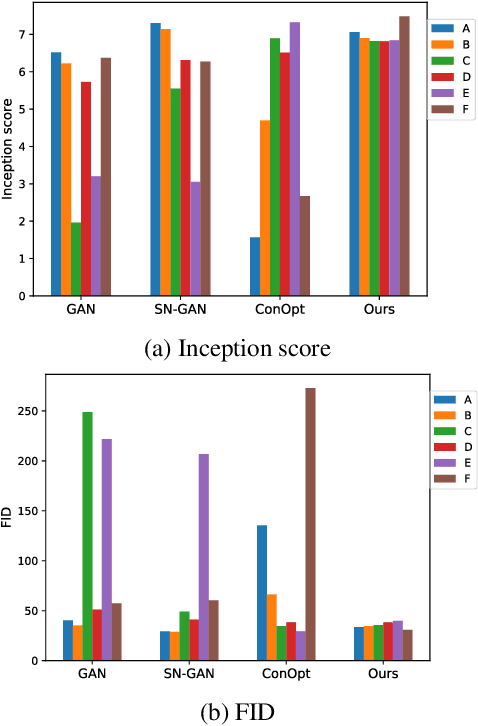
Generative adversarial networks (GANs) are notoriously difficult to train and the reasons for their (non-)convergence behaviors are still not completely understood. Using a simple GAN example, we mathematically analyze the local convergence behavior of its training dynamics in a non-asymptotic way. We find that in order to ensure a good convergence rate two factors of the Jacobian should be \textit{simultaneously} avoided, which are (1) Phase Factor: the Jacobian has complex eigenvalues with a large imaginary-to-real ratio, (2) Conditioning Factor: the Jacobian is ill-conditioned. Previous methods of regularizing the Jacobian can only alleviate one of these two factors, while making the other more severe. From our theoretical analysis, we propose the Jacobian Regularized GANs (JR-GANs), which insure the two factors are alleviated by construction. With extensive experiments on several popular datasets, we show that the JR-GAN training is highly stable and achieves near state-of-the-art results both qualitatively and quantitatively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge