Joint State and Noise Covariance Estimation
Paper and Code
Feb 07, 2025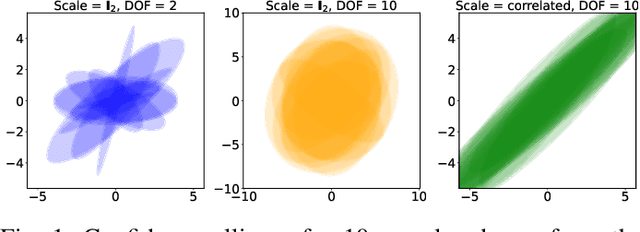
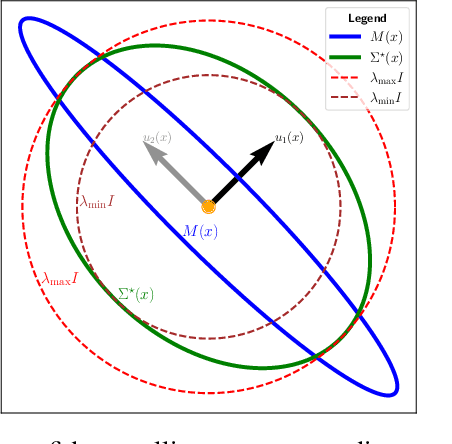
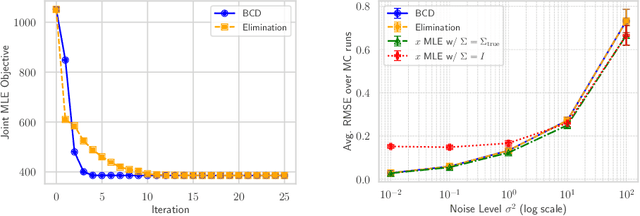
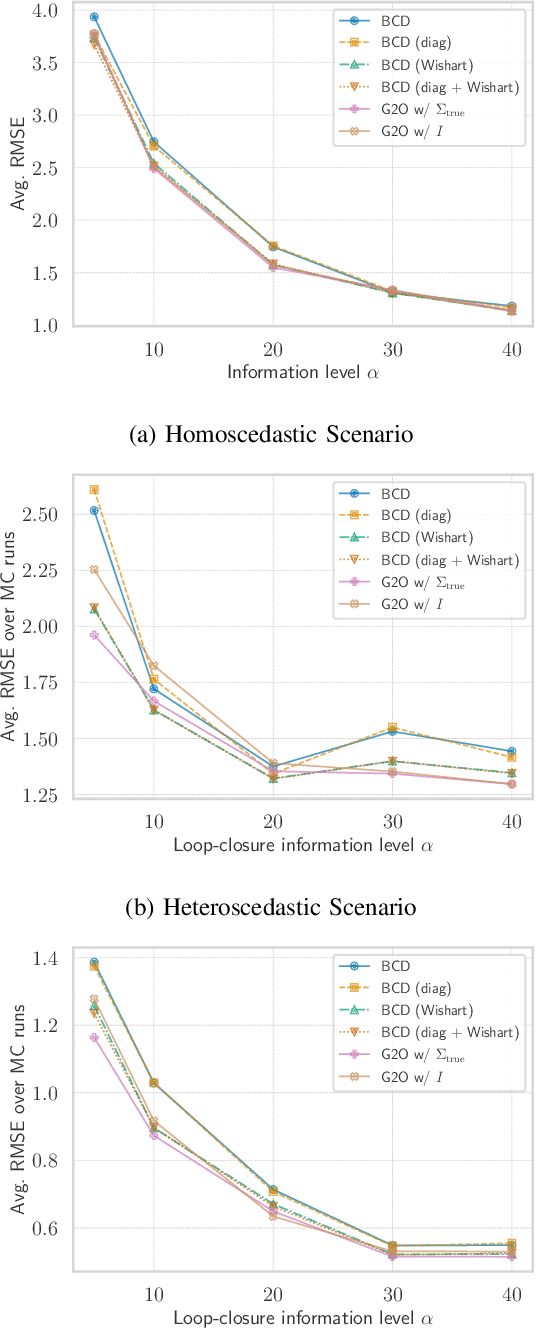
This paper tackles the problem of jointly estimating the noise covariance matrix alongside primary parameters (such as poses and points) from measurements corrupted by Gaussian noise. In such settings, the noise covariance matrix determines the weights assigned to individual measurements in the least squares problem. We show that the joint problem exhibits a convex structure and provide a full characterization of the optimal noise covariance estimate (with analytical solutions) within joint maximum a posteriori and likelihood frameworks and several variants. Leveraging this theoretical result, we propose two novel algorithms that jointly estimate the primary parameters and the noise covariance matrix. To validate our approach, we conduct extensive experiments across diverse scenarios and offer practical insights into their application in robotics and computer vision estimation problems with a particular focus on SLAM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge